Maatriksarvutused joonistamisel
Enamiku joonistamiseks tarvilikku saab välja mõelda põhikoolimatemaatika ning terve talupojamõistuse abil. Kuni on tegemist üksikute paigal seisvate või sirgelt liikuvate punktidega, siis polegi enamasti muud vaja. Kui aga teisendusi ning kujundeid palju saab, siis muutub nii programmi kirjutamine kui töötamine järjest mahukamaks ning tuleb abivahendeid otsida. Keerukama kujundi kuhugi paigutamine taandub enamasti hulga punktide ümbertõstmisele. Keeramise korral tuleb selleks teha töömahukaid trigonomeetrilisi arvutusi. Kui üksteisele järgneb mitu nihutamist ning mitu keeramist, siis kasvab töö maht päris suureks ning suure punktide hulga korral seda enam.
Üheks võimaluseks arvutuste kiirendamisel on tõenäoliselt vaja minevate keerulisemate arvutuste tulemused varem välja arvutada ning neid vajadusel mälust otsida. Kuna siinuse arvutamine on vähemalt tuhat korda aeglasem kui tavaline liitmine või mälust lugemine, siis juba paari tuhande punkti juures on pildi keeramisel vahe märgata. Kuigi põhimõtteliselt võib olla vaja arvutada igasugu nurki, piisab joonistamiste juures siiski enamasti vaid ühekraadisest täpsusest. Nii on vaja eelnevalt välja arvutada siinused vaid 360 kraadi jaoks, asendusvalemeid kasutades võib kergesti piirduda ka veerandiga sellest. Kui veel veidi edasi mõtelda, siis kuna koosinus jookseb siinusest täisnurga jagu taga, siis saab samade 90 kraadi jagu välja arvutatud siinuste abil arvuti tarvis kiirete liitmis-ja lahutustehete abil leida mõlema funktsiooni väärtusi kogu olemasolevas vahemikus.
Graafikaarvutusi saab märgatavalt kiirendada ning osalt grupeerimise teel vähendada maatriksite abil. Muidu kipub nende sageli õppekavas kohustuslike tabelitega suhteliselt vähe igapäevaülesannete juures otse peale hakata olema, aga kui on vaja vähegi keerukamaid kujundeid pinnal või ruumis ümber paigutada, siis parajasti sobiva abiliidese puudumisel jõuab lõpuks paratamatult maatriksiteni välja. Silma on hakanud nende järgmised head omadused:
Iga operatsiooni saab kirjeldada ühe maatriksina ning järjestikused operatsioonid saab ühendada lihtsalt üksteise järel seisvaid maatrikseid korrutades. Lähemad selgitused näidete varal.
Väike meeldetuletus, kuidas maatrikseid korrutatakse. Korrutatavad maatriksid paremal ning vastus vasakul. Vasakpoolse maatriksi ridadel asuvad elemendid korrutatakse parempoolse maatriksi vastavatel veergudel olevate väärtustega. Sellest järeldub, et korrutamisel peab olema vasakpoolse maatriksi ridu sama palju kui parempoolse maatriksi veerge ning korrutise tulemusena tekkivas maatriksis on ridu nii palju kui esimeses ja veerge nagu teises maatriksis.
![]()
Samad väärtused õnnestub korrutada, kui maatriksite read ja veerud ning järjekord vahetada.
![]()
Arvutades koordinaate ümber järgneva valemi järgi
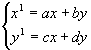 , saab selle kirja panna maatriksitena
, saab selle kirja panna maatriksitena ![]() .
.
Kui punkte on vaja üle kanda korraga rohkem kui üks, siis saab selle ette võtta järgmise korrutise abil:
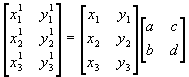 . Iga punkti kohta tuleb lihtsalt esimeses maatriksis üks rida.
. Iga punkti kohta tuleb lihtsalt esimeses maatriksis üks rida.
Arvestades enne toodud üldvalemit, saab välja tuua mõned erijuhud.
![]() ehk uue x-i arvutamisel on vana x-i kordaja 1 ning uue y-i arvutamisel on vana y-i kordaja 1, pikemalt
ehk uue x-i arvutamisel on vana x-i kordaja 1 ning uue y-i arvutamisel on vana y-i kordaja 1, pikemalt 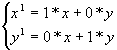 ehk
ehk 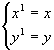 ehk koordinaadid jäävad muutumatuks.
ehk koordinaadid jäävad muutumatuks.
![]() ehk
ehk 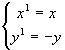 ehk y-koordinaat muutub vastupidiseks ning punkt või joonis peegeldatakse x-telje suhtes. Soovides järjestikku kõigepealt venitada joonist x-telge pidi kaks korda pikemaks
ehk y-koordinaat muutub vastupidiseks ning punkt või joonis peegeldatakse x-telje suhtes. Soovides järjestikku kõigepealt venitada joonist x-telge pidi kaks korda pikemaks ![]() ning seejärel y-telge pidi kaks korda pikemaks
ning seejärel y-telge pidi kaks korda pikemaks ![]() , võib kõigepealt kaks tekkinud muutust kokku korrutada
, võib kõigepealt kaks tekkinud muutust kokku korrutada ![]() ehk
ehk ![]() ning alles siis punkti koordinaadid tulemusega läbi korrutada ning otse lõpptulemus saada.
ning alles siis punkti koordinaadid tulemusega läbi korrutada ning otse lõpptulemus saada.
Järgnevalt koodinäide, kuidas etteantud maatriksi järgi algsetel koordinaatidel asuvat ringi uude kohta transportida valemi järgi x1=2x ning y1=-y. Maatriksiks on 2x2 algväärtustatud massiiv nimega m. Muutujad x ja y tähistavad punkti algseid koordinaate, keskx ja kesky näitavad joonistatava ala keskpunkti ekraanipunktides ning neid läheb vaja vaid joonistamisel. Meetod joonistaTeljed tõmbab ekraanile keskpunktis ristuvad horisontaal- ning vertikaaljoone. Käsk joonistaKujund loob etteantud koordinaatidele ringi, nii et ringi keskpunkt jääb soovitud kohale. Joonistamise arvutamine jääb käsu paint sisse. Uued koordinaadid leitakse algseid muutusmaatriksiga korrutades![]() . Lahtiseletatult korrutatakse algsed koordinaadid x ja y kõigepealt parempoolse maatriksi vasakpoolse veeru väärtustega ning tulemuseks saadakse uue x-i koordinaat x1. Edasi korrutatakse algsete koordinaatide maatriks teisendusmaatriksi parema veeruga ning saadakse uus y-koordinaat y1.
. Lahtiseletatult korrutatakse algsed koordinaadid x ja y kõigepealt parempoolse maatriksi vasakpoolse veeru väärtustega ning tulemuseks saadakse uue x-i koordinaat x1. Edasi korrutatakse algsete koordinaatide maatriks teisendusmaatriksi parema veeruga ning saadakse uus y-koordinaat y1. ![]() . Kui tühjad liikmed maha arvata, siis jääb järele
. Kui tühjad liikmed maha arvata, siis jääb järele![]() , ehk tulemus, mida soovisimegi saavutada.
, ehk tulemus, mida soovisimegi saavutada.
Massiivile võib anda elemendid algväärtustamisel. Kui ühemõõtmelise massiivi algväärtustamisel võis väärtused paigutada lihtsalt komadega eraldatult loogeliste sulgude vahele, siis kahemõõtmelise puhul tuleb ka iga rida eraldi loogeliste sulgude vahele panna ning komadega eraldada. Nii nagu veergude elemendid on üksteisest komadega eraldatuna rida moodustavas plokis, nii loovad read üheskoos komadega eraldatult ridade massiivi ning kokku tulebki kahemõõtmeline massiiv, kus esimene indeks näitab rea- ning teine veeru numbrit.
int[][] m=new int[][]{
{2, 0}, //teisendus x=2x
{0, -1} // y=-y
};
Korrutamine (uue x-i ja y-i arvutamine):
int ux=x*m[0][0]+y*m[1][0];
int uy=x*m[0][1]+y*m[1][1];
Kuna massiivi elemendid algavad nullist, siis on maatriksi esimese rea number 0, teise rea number 1, samuti veergude puhul. Nii korrutataksegi uue x-i leidmiseks kõigepealt vana x maatriksi esimese veeru esimese elemendiga ning siis liidetakse tulemusele vana y-i korrutis teise rea esimese elemendiga. Uue y-i leidmisel sama lugu, vaid korrutatakse algsed x ja y maatriksi teise veeru elementidega. Kogu programm näeks välja järgmine:
import java.applet.Applet;
import java.awt.*;
public class Maatriks1 extends Applet{
int[][] m=new int[][]{ //teisendus x=2x
{2, 0}, // y=-y
{0, -1}
};
int x=30, y=10;
int keskx=150, kesky=150;
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, x, y);
int ux=x*m[0][0]+y*m[1][0];
int uy=x*m[0][1]+y*m[1][1];
g.setColor(Color.blue);
joonistaKujund(g, ux, uy);
}
public static void main(String argumendid[]){
Frame f=new Frame();
f.add(new Maatriks1());
f.setSize(300, 300);
f.setVisible(true);
}
}
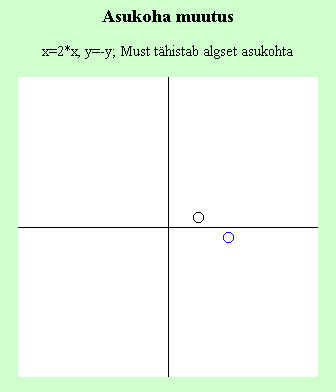
Klass maatriksarvutuste tarvis.
Kui teisendusi tuleb programmi sisse enam, siis kõiki ükshaaval lahti kirjutades tuleb arvutuste peale kokku ikka palju ridu ning maatriksite lisamine ei pruugigi kuigi palju kasu tuua, pigem lihtsalt veel üks tülin juures millega arvestada. Mida rohkem ridu programmis, seda kergem on ka kusagile vigu teha. Enamlevinumate maatriksarvutuste ning ka maatriksi andmete hoidmiseks võib paaril lehel kirjutada vastava klassi või kirjutuslaiskuse puhul enesele võrgu pealt sobiv otsida. Siin näites on loodud klass suvalise soovitavate ridade ja veergude arvuga maatriksi tarvis. Peotäis konstruktoreid enamlevinud kujul andmete sisestamiseks ning meetod kahe maatriksi korrutamiseks, tegevus, mida graafikaarvutuste puhul enim vaja läheb. Lisaks staatilised meetodid üherealise maatriksi loomiseks, et kergemini punkti asukohta määravat maatriksit koostada. Nagu korrutamise puhul näha, tuleb seal kokku kolm tsüklit üksteise sisse paigutada. Kaks tükki ridade ning veergude läbi käimiseks ning kolmas, et arvutatava lahtri tarvis tehtavad korrutised kokku liita. Maatriksi sees olevaid andmeid hoitakse ja arvutatakse reaalarvudena arvutuste täpsuse huvides, joonistamise koordinaadid neile vastavatest pesadest aga küsitakse välja täisarvudena, et oleks kergem tulemusi täisarvulistele ekraanikoordinaatidele paigutada.
public class Maatriks{
double m[][];
public Maatriks(int ridu, int veerge){
m=new double[ridu][veerge];
}
public Maatriks(double a11, double a12, double a21, double a22){
m=new double[][]{
{a11, a12},
{a21, a22}
};
}
public Maatriks(
double a11, double a12, double a13,
double a21, double a22, double a23,
double a31, double a32, double a33
){
m=new double[][]{
{a11, a12, a13},
{a21, a22, a23},
{a31, a32, a33}
};
}
/**
* Luuakse ühe rea ning kahe veeruga maatriks, algväärtusteks parameetritena
* antud väärtused. Tarvitatakse arvutigraafikas tasandil suurendamise
* ning keeramise tarvis.
*/
static Maatriks XY(double x, double y){
Maatriks m1=new Maatriks(1, 2);
m1.m[0][0]=x;
m1.m[0][1]=y;
return m1;
}
static Maatriks XYZ(double x, double y, double z){
Maatriks m1=new Maatriks(1, 3);
m1.m[0][0]=x;
m1.m[0][1]=y;
m1.m[0][2]=z;
return m1;
}
public int X(){ return (int)m[0][0];}
public int Y(){ return (int)m[0][1];}
public int ridadeArv(){return m.length;}
public int veergudeArv(){return m[0].length;}
public Maatriks korruta(Maatriks m2){
if(veergudeArv()!=m2.ridadeArv())
throw new ArithmeticException("Vigane maatriksite suurus "+
veergudeArv()+" "+m2.ridadeArv());
Maatriks m3=new Maatriks(ridadeArv(), m2.veergudeArv());
for(int i=0; i<m3.ridadeArv(); i++){
for (int j=0; j<m3.veergudeArv(); j++){
for(int k=0; k<m3.veergudeArv(); k++){
m3.m[i][j]+=m[i][k]*m2.m[k][j];
}
}
}
return m3;
}
}
Võrreldes algse näitega muutub nüüd programmi põhiosa lihtsamaks ja lühemaks, sest pole enam vaja arvutusi koodi sisse kirjutada, nende eest hoolitseb eraldi klass. Nii algse asukoha kui muutuse saab kirjeldada maatriksina ning uus asukoht leitakse nende korrutisena. Kui eespool seisvat maatriksi klassi vaadata, siis nelja parameetriga konstruktori puhul loetakse kaks esimest esimese rea ning kaks järgmist maatriksi teise rea väärtusteks.
import java.applet.Applet;
import java.awt.*;
public class Maatriks2 extends Applet{
Maatriks muutus=new Maatriks(2, 0, 0, -1);
Maatriks asukoht=Maatriks.XY(30, 10);
int keskx=150, kesky=150;
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, asukoht.X(), asukoht.Y());
Maatriks uuskoht=asukoht.korruta(muutus);
g.setColor(Color.blue);
joonistaKujund(g, uuskoht.X(), uuskoht.Y());
}
}
Keeramine
Soovides algset punkti ümber koordinaattelgede keskpunkti keerata, võib kasutada teisendusmaatriksit ![]() , kus a on soovitava keeramise nurk. Erijuhul, kui soovitakse keerata täisnurga jagu vastupäeva, tuleb teisenduseks
, kus a on soovitava keeramise nurk. Erijuhul, kui soovitakse keerata täisnurga jagu vastupäeva, tuleb teisenduseks ![]() ehk x=-y ning y=x. All näites pööratakse PI/6 ehk 30o.
ehk x=-y ning y=x. All näites pööratakse PI/6 ehk 30o.
import java.applet.Applet;
import java.awt.*;
public class Maatriks3 extends Applet{
double nurk=Math.PI/6;
Maatriks muutus=new Maatriks(
Math.cos(nurk), Math.sin(nurk),
-Math.sin(nurk), Math.cos(nurk)
);
Maatriks asukoht=Maatriks.XY(30, 10);
int keskx=150, kesky=150;
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, asukoht.X(), asukoht.Y());
Maatriks uuskoht=asukoht.korruta(muutus);
g.setColor(Color.blue);
joonistaKujund(g, uuskoht.X(), uuskoht.Y());
}
}
Nagu ennist kirjas, juhul kui soovitakse mitu muutust lisada ühtejärge, siis tuleb vastavate muutuste maatriksid lihtsalt ühtejärge kokku korrutada ning tulemuseks on soovitud muutusi sisaldav maatriks, millega algseid koordinaate läbi korrutades saab ühekorrga lõpptulemusele vastavad punktid teada. Mõnikord on muutuste järjekord tähtis nagu ka allpoololevas näiteks. Kokkuvõtlik nihe koosneb keeramisest ning x-koordinaadi korrutamisest koefitsiendiga. Kui näiteks x-telje lähedal asuva punkti koordinaate kõigepealt paarkümmend kraadi ümber keskpunkti keerata ning seejärel x-i väärtust mõne korra suurendada, siis lõpppunkti y jääb sama suureks kui see oli pärast keeramist. Kui aga kõigepealt x-i suurendada ning alles seejärel sama suure nurga jagu keerata, siis lõpptulemuse y on tõenäoliselt tunduvalt suurem kui eelmisel juhul, sest kui pikemat maas olevat latti sama nurga jagu püstipoole kallutada, siis tõuseb tema ots kõrgemale kui lühikese lati puhul.
Juurde on lisatud kerimisribad, et kasutaja saaks kergemini nurka ning suurendust muuta. Iga kerimisriba liigutuse peale arvutatakse uuesti välja muutuse jaoks tarvilikud maatriksid ning tulemus joonistatakse uuesti ekraanile.
import java.applet.Applet;
import java.awt.*;
import java.awt.event.*;
public class Maatriks4 extends Applet implements AdjustmentListener{
Scrollbar nurgasb=new Scrollbar(Scrollbar.HORIZONTAL, 314, 10, 0, 628);
Scrollbar suurendusesb=new Scrollbar(Scrollbar.HORIZONTAL, 110, 10, 0, 200);
Maatriks muutus;
Maatriks asukoht=Maatriks.XY(30, 10);
int keskx=150, kesky=150;
public Maatriks4(){
Panel p1=new Panel(new GridLayout(2, 2));
p1.add(new Label("Nurk:"));
p1.add(nurgasb);
p1.add(new Label("Suurendus x:"));
p1.add(suurendusesb);
nurgasb.addAdjustmentListener(this);
suurendusesb.addAdjustmentListener(this);
setLayout(new BorderLayout());
add(p1, BorderLayout.SOUTH);
arvutaMuutus();
}
void arvutaMuutus(){
double nurk=(nurgasb.getValue()-314)/100.0;
Maatriks nurgam=new Maatriks(
Math.cos(nurk), Math.sin(nurk),
-Math.sin(nurk), Math.cos(nurk)
);
double suurendus=(suurendusesb.getValue()-100)/10.0;
Maatriks suurendusem=new Maatriks(
suurendus, 0,
0, 1
);
muutus=nurgam.korruta(suurendusem); //enne keerab, siis suurendab
// muutus=suurendusem.korruta(nurgam); //enne suurendab, siis keerab
repaint();
}
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, asukoht.X(), asukoht.Y());
Maatriks uuskoht=asukoht.korruta(muutus);
g.setColor(Color.blue);
joonistaKujund(g, uuskoht.X(), uuskoht.Y());
}
public void adjustmentValueChanged(AdjustmentEvent e){
arvutaMuutus();
}
}
Nihutamine
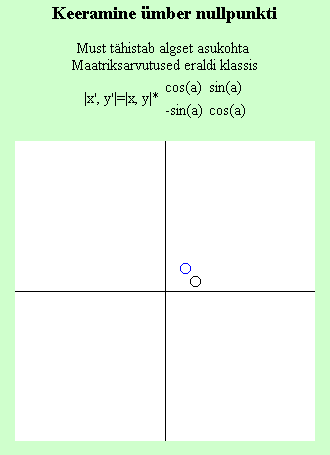
Kahemõõtmelise punkti nihutamiseks läheb tarvis kolmemõõtmelist maatriksit, kahemõõtmelisest ei piisa. Et punkti koordinaate annaks sellise maatriksiga läbi korrutada, tuleb ka seal kolmas suurus juurde võtta. Punkt muudetakse ruumiliseks, andes talle z-i väärtuseks 1. Nõnda, kui soovida punkti asukohaga x, y nihutada paika x1, y1, tuleks kasutada järgmist teisendust: 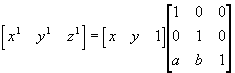 , kus a ning b väärtused tähistavad vastavalt x ning y koordinaatide nihet vastavaid telgi pidi. Ka muud siiamaani kasutatud teisendused võib samaks jätta, kasutades vaid maatriksi esimest kaht rida ning veergu ning jättes z-koordinaadi väärtuseks ning kordajaks arvu 1. Nii näiteks näeks kolmemõõtmeliste maatriksitena arvutatult ümber nullpunkti tasandil (ehk ümber z-telje ruumis) keeramine välja
, kus a ning b väärtused tähistavad vastavalt x ning y koordinaatide nihet vastavaid telgi pidi. Ka muud siiamaani kasutatud teisendused võib samaks jätta, kasutades vaid maatriksi esimest kaht rida ning veergu ning jättes z-koordinaadi väärtuseks ning kordajaks arvu 1. Nii näiteks näeks kolmemõõtmeliste maatriksitena arvutatult ümber nullpunkti tasandil (ehk ümber z-telje ruumis) keeramine välja 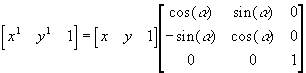 ning tulemused on samade nurkade puhul samad, kui kahemõõtmelise maatriksiga arvutades. Nõnda selgub ka avaldisele otsa vaadates, sest võrreldes eelmise väiksema arvutusega lisandub x-i ning y-i arvutamisel vaid liige 1*0, mis väärtuse 0 tõttu lõpptulemust ei muuda. Suuresti arvutigraafikas kasutataksegi 3*3 muutusmaatrikseid, sest nii on võimalik kõik enamasti ette tulevad teisendused ühesuguse suurusega tabelitesse kokku panna ning pole muret kahest mõõtmest kolme või pärast tagasi ülekandmise juures.
ning tulemused on samade nurkade puhul samad, kui kahemõõtmelise maatriksiga arvutades. Nõnda selgub ka avaldisele otsa vaadates, sest võrreldes eelmise väiksema arvutusega lisandub x-i ning y-i arvutamisel vaid liige 1*0, mis väärtuse 0 tõttu lõpptulemust ei muuda. Suuresti arvutigraafikas kasutataksegi 3*3 muutusmaatrikseid, sest nii on võimalik kõik enamasti ette tulevad teisendused ühesuguse suurusega tabelitesse kokku panna ning pole muret kahest mõõtmest kolme või pärast tagasi ülekandmise juures.
Järgnevas näites paistabki, kuidas algse punkti koordinaati kümne punkti jagu paremale ning kolmekümne jagu üles nihutada. Loomulikult saaks selle toiminguga ilma maatriksiketa tunduvalt lihtsamalt toime, kuid nii on täiendav vahend komplektis juures, mida on võimalik ühes teiste omasugustega suurest hulgast punktides koosneva kujundi asendi muutmiseks kasutada.
import java.applet.Applet;
import java.awt.*;
public class Maatriksnihe extends Applet{
double nihkex=10, nihkey=30;
Maatriks muutus=new Maatriks(
1, 0, 0,
0, 1, 0,
nihkex, nihkey, 1
);
Maatriks asukoht=Maatriks.XYZ(30, 10, 1);
int keskx=150, kesky=150;
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, asukoht.X(), asukoht.Y());
Maatriks uuskoht=asukoht.korruta(muutus);
g.setColor(Color.blue);
joonistaKujund(g, uuskoht.X(), uuskoht.Y());
}
}
Keeramine ümber määratud punkti.
Otseselt lihtsat valemit keskkohast erineva punkti ümber keeramiseks pole, selline vajadus kipub aga kirjutamise jooksul ikka tekkima. Olgu või tegemist ekraanil jalutava kilponnaga (millega paratamatult puutub kokku näiteks joonistavas programmeerimiskeeles LOGO), kes soovib mingis punktis esese asendit ning liikumissuunda muuta. Üheks võimaluseks on pidevalt joonistamisel hoida meeles kilpkonna enese keskkohta ning jalgu joonistada arvestades keskpunktist. Tahtes aga arvutamist universaalsemaks teha ning mitte pidevalt hoida meeles ning kasutada arvutamisel topeltkoordinaate, võib koostada maatriksi ka ümber määratud punkti keeramiseks. Selle saab luua, kasutades järgemööda olemasolevaid oskusi. Kõigepealt tuleb soovitav pöördekeskpunkt nihutada nullpunkti. Ümber nullpunkti keeramine käib lihtsa tuttava arvutuse teel ning kujundi (näiteks kilpkonna) õigesse algsesse kohta tagasi paigutamiseks tuleb taas kõik punktid vajaliku nihke jagu tagasi liigutada. Mujalgi toimiv reegel, et kui mõnda asja on liialt keeruline teha, siis püüa see jagada tuttavateks alamtöödeks ning nendega ükshaaval hakkama saada. Ega siis tulemuski tulemata ei jää. Matemaatiliselt näeks selline nullpunkti nihutamine, keeramine ja tagasi nihutamine välja järgnevalt, tähistades a ja b-ga keeramise keskkohta ning x-i ja y-ga keeratava punkti asukohti.
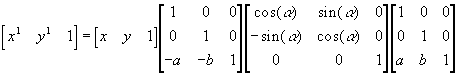
Kui üle kanda on rohkem kui üks punkt, siis võib arvutuse kiiruse huvides kõigepealt tagumised kolm maatriksit kokku korrutada üheks muutusmaatriksiks ning siis esimest koordinaatide maatriksit tekkinud muutustemaatriksiga läbi korrutades saame sama väikese arvutuskuluga teada uued koordinaadid, ükskõik kui keeruline ka tehtav nihe peaks olema. Kui tegemist on 3x3 reaalarvumaatriksiga, siis on arvuti jaoks ükskõik, kui ümmargused seal sees paiknevad arvud juhtuvad olema. Ning kõik tänu maatriksite korrutamise assotsiatiivsuse seadusele, mis ütleb, et (M1M2)M3 =M1(M2M3). Nii saab tagumised muutusmaatriksid varakult tagavaraks ära korrutada ning samu teisendusi nii palju kordi rakendada, kui palju algseid asukohti ümber tõsta on.
Sama algoritmi realiseering programmina. Keeramise keskpunkti saab kasutaja hiirega määrata, samuti kerimisriba abil muuta nurka, kui palju algse asendiga võrreldes keerata.
import java.applet.Applet;
import java.awt.*;
import java.awt.event.*;
public class Maatriks4a extends Applet implements AdjustmentListener{
Scrollbar nurgasb=new Scrollbar(Scrollbar.HORIZONTAL, 314, 10, 0, 628);
Maatriks muutus;
Maatriks asukoht=Maatriks.XYZ(30, 10, 1);
Maatriks keermekeskus=Maatriks.XYZ(50, 30, 1);
int keskx=150, kesky=150;
public Maatriks4a(){
Panel p1=new Panel(new GridLayout(1, 2));
p1.add(new Label("Nurk:"));
p1.add(nurgasb);
nurgasb.addAdjustmentListener(this);
setLayout(new BorderLayout());
add(p1, BorderLayout.SOUTH);
addMouseListener(
new MouseAdapter(){
public void mousePressed(MouseEvent e){
keermekeskus=Maatriks.XYZ(
e.getX()-keskx,
-(e.getY()-kesky), 1
);
arvutaMuutus();
}
}
);
arvutaMuutus();
}
void arvutaMuutus(){
double nurk=(nurgasb.getValue()-314)/100.0;
Maatriks nurgam=new Maatriks(
Math.cos(nurk), Math.sin(nurk), 0,
-Math.sin(nurk), Math.cos(nurk), 0,
0, 0, 1
);
Maatriks keskelenihe=new Maatriks(
1, 0, 0,
0, 1, 0,
-keermekeskus.X(), -keermekeskus.Y(), 1
);
Maatriks paikanihe=new Maatriks(
1, 0, 0,
0, 1, 0,
keermekeskus.X(), keermekeskus.Y(), 1
);
muutus=keskelenihe.korruta(nurgam).korruta(paikanihe);
repaint();
}
public void joonistaTeljed(Graphics g){
g.drawLine(keskx, 0, keskx, 2*kesky);
g.drawLine(0, kesky, 2*keskx, kesky);
}
public void joonistaKujund(Graphics g, int kx, int ky){
g.drawOval(keskx+kx-5, kesky-ky-5, 10, 10);
}
public void paint(Graphics g){
joonistaTeljed(g);
joonistaKujund(g, asukoht.X(), asukoht.Y());
Maatriks uuskoht=asukoht.korruta(muutus);
g.setColor(Color.blue);
joonistaKujund(g, uuskoht.X(), uuskoht.Y());
g.setColor(Color.green);
joonistaKujund(g, keermekeskus.X(), keermekeskus.Y());
}
public void adjustmentValueChanged(AdjustmentEvent e){
arvutaMuutus();
}
}
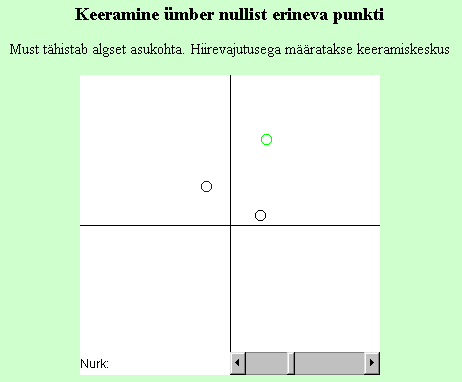
Pööramine ümber telgede.
Kui pööramine xy tasandil ehk ümber z-telje käis maatriksi järgi 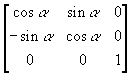 , siis on näha, et peadiagonaalil on telje, mille ümber pöörati, väärtuseks 1. Ridade ja veergude muud elemendid, mis selle koordinaadiga seotud, on nullid. Sarnaselt pööratakse ka ümber teiste telgede. Ümber x-i
, siis on näha, et peadiagonaalil on telje, mille ümber pöörati, väärtuseks 1. Ridade ja veergude muud elemendid, mis selle koordinaadiga seotud, on nullid. Sarnaselt pööratakse ka ümber teiste telgede. Ümber x-i 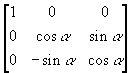 ning ümber y-i
ning ümber y-i 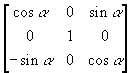 . Kui tahame kõik koordinaatteljed pidada nullpunktist eemalduvatena, siis arvestades kruvireegli järgi, et päripäeva keeramine viib edasi ja vastupäeva tagasi, tuleks tegemist xy, yz ning zx tasanditega ning ümber y-telje keeramise maatriks tuleks siis vastassuunaline ehk
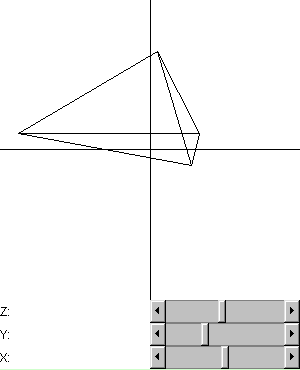
. Kui tahame kõik koordinaatteljed pidada nullpunktist eemalduvatena, siis arvestades kruvireegli järgi, et päripäeva keeramine viib edasi ja vastupäeva tagasi, tuleks tegemist xy, yz ning zx tasanditega ning ümber y-telje keeramise maatriks tuleks siis vastassuunaline ehk 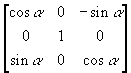 . Mitut teisendust üheskoos rakendades on oluline teisenduste järjekord. Kui kõigepealt pööratata ümber z-i ning seejärel pöörata ümber y-i, siis keerata enam mitte ümber algse kujundi y-telje, vaid pärast esimest pööret asetunud kujundi y-telje. All näites saab kerimisribade abil määrata, kui palju joonistatav tetraeeder ümber millise telje keeratud on. Kui ribad asuvad keskel, siis on kõik pöördenurgad nullid ning kujund algasendis. Koodis leitakse vastavalt iga kerimisriba asendile vastava telje suhtes pöörav muutusmaatriks ning siis korrutatakse muutused kokku.
. Mitut teisendust üheskoos rakendades on oluline teisenduste järjekord. Kui kõigepealt pööratata ümber z-i ning seejärel pöörata ümber y-i, siis keerata enam mitte ümber algse kujundi y-telje, vaid pärast esimest pööret asetunud kujundi y-telje. All näites saab kerimisribade abil määrata, kui palju joonistatav tetraeeder ümber millise telje keeratud on. Kui ribad asuvad keskel, siis on kõik pöördenurgad nullid ning kujund algasendis. Koodis leitakse vastavalt iga kerimisriba asendile vastava telje suhtes pöörav muutusmaatriks ning siis korrutatakse muutused kokku.
muutus=mz.korruta(my).korruta(mx);