Graafiku koostamine.

Joonistuskäsud, ekraanikoordinaadid, maailmakoordinaadid, skaala, ümardamine

Mõnikord tavatsetakse öelda, et üks pilt on rohkem väärt kui tuhat sõna. Ei pruugi see alati kehtida, kuid joonistest võib vahel kasu küll olla. Kui andmed ei muutu, siis kannatab mõne vastavaotstarbelise programmiga pildid valmis teha ning tekstile juurde liita. Kui aga andmed muutuvad või ei olda olemasoleva programmi poolt pakutava väljundiga rahul, siis on põhjust ise koodilõik kirjutada, mis andmed jooniseks muundab.

Nagu programmide ja ka muude toimingute puhul, alustame lihtsamast ja liigume keerulisema suunas. Näited tehakse pideva ruutfunktsiooni tarvis, kuid sarnased arvutused tuleb ka muul puhul ette võtta, kui oma andmetele vastavalt püüame miskit ekraanile paigutada.

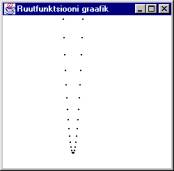
Üksikud ekraanipunktid.

Joonistamisel samastatakse graafiku matemaatilised maailmakoordinaadid ning arvuti ekraanikoordinaadid. Funktsiooni väärtus arvutatakse täisarvuliste x-ide juures ning vastavale x ja y kombinatsiooniga määratud kohale joonistatakse täpike.

import java.awt.*; import java.applet.*; public class Graafik1 extends Applet{ public void paint(Graphics g){ for(int x=0; x<100; x++){ g.drawOval(x, x*x, 1, 1); } } }

Nihutus ja keeramine

Üksühene arvutuskoordinaatide ja ekraanipunktide vastavus võib küll mugav koodiks kirjutada olla ning esmase pildi selle abil ka saab, kuid selline telgede asetus võib arvutigraafikast kaugemal seisvale vaatajale harjumatu ning võõrastav tunduda. Samuti tekivad probleemid x-i ja y-i negatiivsete väärtuste juures, sest neid pole lihtsalt näha. Veidi mugavam peaks olema järgmine lähend:

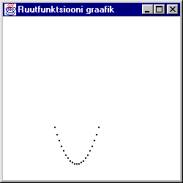
Üks ühik graafikul vastab endiselt ekraanipunktile. Joonist aga nihutati x-teljel 100 punkti võrra paremale ja y-teljel 200 punkti võrra allapoole ning y-telje kasvamise suund keerati vastupidiseks.

Ekraani y-punkti arvutamisel lahutatakse kahesajast maha graafikul oleva igreki väärtus. Kui y=0, siis joonistatakse täpp rakendi y-koordinaadile 200. Kui y>0, siis tuleb 200-y kahesajast väiksem ning täpp ekraanil järelikult kõrgemal. Negatiivse y puhul ületab 200-y kahtsadat ning

tulemuseks on täpp nullpunktist (kahesajast) allpool.

import java.awt.*; import java.awt.geom.*; import java.awt.image.*; import java.applet.*; public class Graafik2 extends Applet{ public void paint(Graphics g){ for(int x=-100; x<100; x++){ g.drawOval(x+100, 200-x*x, 1, 1); } } public static void main(String argumendid[]){ Frame f=new Frame("Ruutfunktsiooni graafik"); f.add(new Graafik2()); f.setSize(250, 250); f.setVisible(true); } }

Mõõtkava.

Koodi sisse trükitud konstandid on asendatud muutujatega. Nii on vähe suurema programmi puhul

kergem näha, millega tegu, sest muutujal on nimi. Samuti, kui sama suurust on kasutatud mitmes kohas, siis muutmisvajaduse korral saab väärtuse määrata ühes kohas ning jääb ära oht, et kusagilt midagi paika muutmata jääb. Põhjalikud programmeerijad soovitavad koguni kõik väärtused (v.a. 0 ja 1)

asendada tähenduslike nimedega muutujatega. Siis teistel koodi lugejatel rohkem

lootust aru saada. Ning mõnikord on mõistlik needki numbrid sõnadega asendada.

Arvutustehe on toodud välja eraldi funktsioonina. Nii on teda kergem mitmest kohast vajadusel välja kutsuda, samuti muuta ja parandada kui vajadust peaks olema.

Koefitsent näitab, mitu ekraanipunkti vastab ühele ühikule graafikul. Kui koefitsent on võrdne ühega, siis graafiku- ning ekraanipunktide arv kattub. Ühest suurema kordaja korral venitatakse ekraanil graafik vastava telje suunas välja. Kui kordaja on 0 ja 1 vahel, siis ekraanijoonist vähendatakse. Ning kui kordaja on alla nulli, siis joonistatakse ekraanil maailmakoordinaatidele vastupidises suunas.

Siin näites y koefitsent -0.5 tähendab, et ekraani- ning graafikuühikud on eri suundades (miinusmärk ees) ning ekraanipunkte on poole vähem kui punkte graafikul. Nii on võimalik kiirelt kasvav ruutfunktsioon ekraanile paremini ära mahutada.

import java.awt.*; import java.applet.*; public class Graafik3 extends Applet{ double minx=-10, maxx=10, samm=1; double koefitsientx=3, koefitsienty=-0.5; //mitu ekraanipunkti vastab ühele ühikule joonisel //miinus vahetab suuna int xnihe=100, ynihe=200; public void paint(Graphics g){ for(double x=minx; x<=maxx; x=x+samm){ g.drawOval(xnihe+(int)( x *koefitsientx), ynihe+(int)(f(x)*koefitsienty), 1, 1); } } double f(double x){ //funktsioon eraldi välja, siis kergem //kasutada ja muuta return x*x; } public static void main(String argumendid[]){ Frame f=new Frame("Ruutfunktsiooni graafik"); f.add(new Graafik3()); f.setSize(250, 250); f.setVisible(true); } }

Pideva joonega graafik

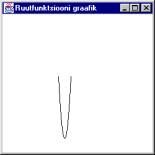
Endiste täppide asemel ühendatakse nüüd punktid omavahel joontega. Kui jooned piisavalt

lühikesed on, siis jääb vaatajale mulje, nagu oleks tegemist kõveraga. Kõigepealt tuleb

välja arvutada esimese punkti asukoht. Seejärel leida teise punkti asukoht ning kahe esimese

punkti vahele tõmmata joon. Siis jäetakse viimatiarvutatud punkt meelde, arvutatakse järgmine, tõmmatakse

taas joon ning jäetakse punkt meelde. Kuni ollakse jõudnud arvutatava lõigu lõpuni.

import java.awt.*; import java.applet.*; public class Graafik4 extends Applet{ public void paint(Graphics g){ int vanax=90; int vanay=100; for(int x=-10; x<=10; x++){ int uusx=x+100; int uusy=200-x*x; g.drawLine(vanax, vanay, uusx, uusy); vanax=uusx; vanay=uusy; } } public static void main(String argumendid[]){ Frame f=new Frame("Ruutfunktsiooni graafik"); f.add(new Graafik4()); f.setSize(250, 250); f.setVisible(true); } }

Komponendi suuruse arvestamine

Head programmid pidavat suutma arvestada ressurssidega, mis neile kättesaadavad on. Et kui mäluga arvutis kitsas, siis hoitakse enam andmeid kettal ja lihtsalt arvutatakse mõnevõrra kauem. Või kui ekraanipinda vähem kasutada, siis jäetakse nähtavale vaid tähtsaimad lõigud. Püüame ka siin niimoodi teha.

Raami suuruse muutmisel arvutatakse pilt uuesti-käivitatakse paint. Nagu näha, seal on töö mitmeks alalõiguks jagatud ning vaid otsesed joonistuskäsud paint'i sisse jäänud. Suurenduseks tarvilikud konstandid leitakse eraldi alamprogrammis, samuti paigutatakse joonise servadesse koordinaadid. Ka maailmakoordinaatide ja ekraanikoordinaatide teisendamiseks on omaette funktsioon loodud. Joonise tarvis arvutatakse välja kõigepealt vasakpoolseim x ja y. Edasi igal järgmisel korral tõmmatakse joon eelmisest punktist uude punkti ning jäetakse uus punkt eelmisena meelde.

public void paint(Graphics g){

leiaKonstandid();

joonistaKoordinaadid(g);

int vanax=ekraaniX(minx);

int vanay=ekraaniY(f(minx));

for(double x=minx; x<=maxx; x=x+samm){

int uusx=ekraaniX(x);

int uusy=ekraaniY(f(x));

g.drawLine(vanax, vanay, uusx, uusy);

vanax=uusx;

vanay=uusy;

}

}

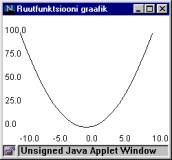
Joonistamisel arvestatakse ekraanipinna suurust ning nii x- kui y-teljel funktsiooni

suurimaid ja vähimaid väärtusi. Selle järele arvutatakse koefitsendid. Siin näites antakse ette x-i vähim ja suurim väärtus ning funktsiooni kõvera punktid arvutatakse iga kahekümnendiku arvutuspiirkonna pikkuse tagant. Et funktsioon ega arvutusvahemik praegu programmi töö ajal ei muutu, saab suurimad ja vähimad väärtused leida juba rakenduse töö algul.

double minx=-10, maxx=10, samm=(maxx-minx)/20;

double miny=minY(), maxy=maxY();

Suurima y-i leidmiseks käiakse lihtsalt kogu funktsioon arvutussammu pikkuste lõikude tagant läbi ning jäetakse meelde suurim väärtus. Tegu pole küll matemaatiliselt päris korrektse lähenemisega, sest võib juhtuda, et kuhugi arvutuskoha vahele satub piik, kus funktsiooni väärtus erineb tunduvalt kõrval asuvatest väärtustest, kuid harilike funktsioonide puhul peaks sellisest lähenemisest piisama.

double maxY(){

double max=f(minx);

for(double x=minx; x<=maxx; x+=samm){

if(f(x)>max)max=f(x);

}

return max;

}

Kui vähimad ja suurimad väärtused olemas, siis edasi tasub leida muud joonistamisel tarvilikud kordajad. Ning põhiliseks määrajaks on sel korral kasutaja ette antud komponendi suurus, mille annab pärida getSize abil. Suurenduskordaja leidmiseks arvutatakse nii x- kui y-suunal väärtuste ulatus maailmakoordinaatides. Edasi leitakse, mitu ekraanikoordinaati selle ala peale jagub. Et ei tekiks jagamist nulliga, on ära määratud vähim ulatus, millest väiksemaks ei või maailmakoordinaatide vahemik minna. Samuti jäetakse ekraanil mõningane servaruum, et joonte otsad päris äärteni välja ei läheks. Ka leitakse funktsiooni nähtavale osale keskpunkt, et oleks võimalik joonis ekraanil suhteliselt ühtlaselt paigutada.

void leiaKonstandid(){

korgus=getSize().height;

laius=getSize().width;

ulatusx=maxx-minx;

ulatusy=maxy-miny;

if(ulatusx<ulatusmin)ulatusx=ulatusmin;

if(ulatusy<ulatusmin)ulatusy=ulatusmin;

koefitsientx=(laius-2*servaruum)/ulatusx;

koefitsienty=-(korgus-2*servaruum)/ulatusy;

keskx=(maxx+minx)/2;

kesky=(maxy+miny)/2;

}

Ka servadesse koordinaatide joonistamiseks on loodud eraldi meetod. Laiust pidi on jäetud iga väärtuse tarvis 40 ja kõrgust pidi 30 punkti. Selle järgi leitakse, mitu väärtust kummassegi jadasse paigutatakse. Edasi leitakse piirkonnas ühtlaste vahede järgi väärtused ning joonistatakse ekraanile.

Arvutus minx+i/(double)numbreidx*(maxx-minx) lahti seletatult: maxx-minx on x-i väärtuste vahemik. i on joonistatava väärtuse järjekorranumber. i/numbreidx näitab suhte, kui kaugel väärtuste joonistamisega ollakse. Tüübimuundur (double) väärtuse numbreidx ees hoolitseb, et jagataks reaalarvuliselt. Kuna nii i kui numbreidx on täisarvulised, siis Java antaks vastuseks ka täisarv ehk nende arvude suhte täisosa. i/(double)numbreidx*(maxx-minx) näitab seega x-ide vahemiku läbitud vahemaad ning minx sinna otsa liidetult annab i-nda joonisel oleva arvu väärtuse.

void joonistaKoordinaadid(Graphics g){

int numbreidy=(korgus-2*servaruum)/30;

int numbreidx=(laius-2*servaruum)/40;

for(int i=0; i<=numbreidx; i++){

double x=umarda(minx+i/(double)numbreidx*(maxx-minx), 2);

g.drawString(x+"", ekraaniX(x), korgus-5 );

}

for(int i=0; i<=numbreidy; i++){

double y=umarda(miny+i/(double)numbreidy*(maxy-miny), 2);

g.drawString(y+"", 3, ekraaniY(y));

}

}

Käsklus määratud arvu kümnendkohtadega ümardamiseks, mida Javas vaikimisi kujul sisse ehitatud pole korrutab arvu kõigepealt kümne astmega, mitu kohta tahetakse koma taha jätta. Seejärel ümardatakse round-käsuga täisosani ning edasi jagatakse tulemus arvu 10 vastava astmega.

double umarda(double arv, int kohti){

return(Math.round(arv*Math.pow(10, kohti))/Math.pow(10, kohti));

}

Et veebilehel oleval rakendil kannataks joonistatava ala suurust muuta, on üheks võimaluseks paigutada joonis eraldi aknaraami. Et iseseisva programmi puhul käivitus juba ilusti main-meetodi abil töötab, siis kannatab rakendist see valmisolev programm kogu täiega välja kutsuda. Käsurealt võetavaid ja mainile ette antavaid parameetreid siin kusagilt võtta pole. Et aga main on tavaline alamprogramm ning üldjuhul kannatab muutujale ette anda ka lihtsalt tühiväärtuse, siis kutsutakse põhiprogramm välja käsuga Graafik5.main(null).

import java.applet.Applet;

import java.awt.*;

import java.awt.event.*;

public class Graafik5Rakend extends Applet{

Button nupp=new Button("Ava graafik");

public Graafik5Rakend(){

setLayout(new BorderLayout());

add(nupp, BorderLayout.CENTER);

nupp.addActionListener(new ActionListener(){

public void actionPerformed(ActionEvent e){

Graafik5.main(null);

}});

}

}

Ning lõpuks joonistuslõuendi kood tervikuna.

import java.awt.*;

import java.awt.event.*;

public class Graafik5 extends Canvas{

double minx=-10, maxx=10, samm=(maxx-minx)/20;

double miny=minY(), maxy=maxY();

double ulatusmin=0.01, ulatusx, ulatusy;

int korgus, laius;

int servaruum=25;

double koefitsientx, koefitsienty, keskx, kesky;

public void paint(Graphics g){

leiaKonstandid();

joonistaKoordinaadid(g);

int vanax=ekraaniX(minx);

int vanay=ekraaniY(f(minx));

for(double x=minx; x<=maxx; x=x+samm){

int uusx=ekraaniX(x);

int uusy=ekraaniY(f(x));

g.drawLine(vanax, vanay, uusx, uusy);

vanax=uusx;

vanay=uusy;

}

}

int ekraaniX(double matemx){

return laius/2+(int)((matemx-keskx)*koefitsientx);

}

int ekraaniY(double matemy){

return korgus/2+(int)((matemy-kesky)*koefitsienty);

}

double minY(){

double min=f(minx);

for(double x=minx; x<=maxx; x+=samm){

if(f(x)<min)min=f(x);

}

return min;

}

double maxY(){

double max=f(minx);

for(double x=minx; x<=maxx; x+=samm){

if(f(x)>max)max=f(x);

}

return max;

}

void leiaKonstandid(){

korgus=getSize().height;

laius=getSize().width;

ulatusx=maxx-minx;

ulatusy=maxy-miny;

if(ulatusx<ulatusmin)ulatusx=ulatusmin;

if(ulatusy<ulatusmin)ulatusy=ulatusmin;

koefitsientx=(laius-2*servaruum)/ulatusx;

koefitsienty=-(korgus-2*servaruum)/ulatusy;

keskx=(maxx+minx)/2;

kesky=(maxy+miny)/2;

}

void joonistaKoordinaadid(Graphics g){

int numbreidy=(korgus-2*servaruum)/30;

int numbreidx=(laius-2*servaruum)/40;

for(int i=0; i<=numbreidx; i++){

double x=umarda(minx+i/(double)numbreidx*(maxx-minx), 2);

g.drawString(x+"", ekraaniX(x), korgus-5 );

}

for(int i=0; i<=numbreidy; i++){

double y=umarda(miny+i/(double)numbreidy*(maxy-miny), 2);

g.drawString(y+"", 3, ekraaniY(y));

}

}

double umarda(double arv, int kohti){

return(Math.round(arv*Math.pow(10, kohti))/Math.pow(10, kohti));

}

double f(double x){

return x*x;

}

public static void main(String argumendid[]){ final Frame f=new Frame("Ruutfunktsiooni graafik"); f.add(new Graafik5()); f.setSize(250, 250); f.setVisible(true); f.addWindowListener(new WindowAdapter(){ public void windowClosing(WindowEvent e){ f.setVisible(false); System.exit(0); } }); } }

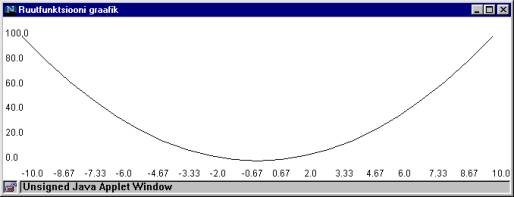
Sama graafik laiemaks venitatuna

Ülesandeid

· Joonista kuupfunktsiooni graafik

· Võimalda kasutajal määrata kordajaid

· Viiruta graafiku joone ja x-telje vaheline ala.