Kolmemõõtmeline graafika

Java3D, koordinaateljestik, kujundid, vaateplatvorm, liikumine

Kolmes mõõtmes kujundite ekraanile paigutamiseks, liigutamiseks ning keeramiseks on Java keelde loodud abivahendite komplekt nimega Java 3D. See tuleb lisaks kompilaatorile/interpretaatorile masinasse installeerida ning seejärel saab temasse kuuluvaid vahendeid kasutada. Kui soovida, et seilur suudaks oma ekraanil selle paketi abil loodud rakendeid näidata, siis tuleb 3D ka brauseri Java virtuaalmasina juurde installeerida. Pea kõike siinse paketi abil loodut õnnestub ka tavavahendite ning keskkooli matemaatika abil lahendada, sest sisuliselt on ju ikka tegemist mingil hetkel ekraanipunktide värvimise ning hiire- ja klaviatuurisündmustele reageerimisega, kuid siin õnnestub veidi arvutamisvaeva kokku hoida ning samuti aitab operatsioonisüsteemi kaudu graafikakaardi/kiirendiga suhtlemine pildi arvutamist ja liigutamist sujuvamaks muuta.

Nagu iga uus asi, on seegi API arenemisjärgus (2001), kuid juba on siinsete vahenditega täiesti võimalik midagi ette võtta. Programmeerija tarvis lisatakse mõniteist paketti hulga klasside ning meetoditega. "Valmis" pakettideks on javax.media.j3d üldisemate klassidega kolmemõõtmeliste kujundite koostamiseks, liigutamiseks ja valgustamiseks. javax.vecmath aitab hoida ja töödelda kolme mõõtme kohta käivaid andmeid. Abipaketid algavad com.sun.j3d-ga ning sealt leiab valmis kujundeid ning muid realisatsioone. Nende pakettide nimed võivad tulevikus tõenäolisemalt muutuda, kuid võimalused ja põhimõtted peaksid ka edaspidi samasuguseks jääma.

Kuna Java3D kasutab operatsioonisüsteemist sõltuvaid vahendeid, siis kuulub kolmemõõtmeline lõuend Canvas3D AWT (mitte Swingi) komponentide hulka. Selle lõuendi sisse saabki oma kolmemõõtmelist programmi ehitama hakata. Lõuendi sees paiknevad objektid tuleb asetada puukujulisse hierarhiasse. Puu juureks on BranchGroup. Sinna külge saab lisada nii kujundeid kui edaspidi ka sõlmi kujundite nihutamiseks ja keeramiseks. SimpleUniverse loob kesta, mille abil ühendab kujundipuu 3D lõuendiga ning hoolitseb kasutaja asukoha eest. Järgnevas näites ilmub ekraanile värviline kuup (õigemini üks külg temast).

import java.applet.Applet;

import java.awt.*;

import com.sun.j3d.utils.geometry.ColorCube;

import com.sun.j3d.utils.universe.SimpleUniverse;

import javax.media.j3d.*;

public class Kuup1 extends Applet {

public Kuup1() {

setLayout(new BorderLayout());

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

add(c, BorderLayout.CENTER);

BranchGroup juur = new BranchGroup();

juur.addChild(new ColorCube(0.5));

juur.compile();

SimpleUniverse u = new SimpleUniverse(c);

u.getViewingPlatform().setNominalViewingTransform();

u.addBranchGraph(juur);

}

public static void main(String[] args) {

Frame f=new Frame("Kuup");

f.add(new Kuup1());

f.setSize(300, 300);

f.setVisible(true);

}

}

Nüüd veidi lähem seletus.

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

loob 3D lõuendi vaikeparameetritega, et saaks järgnevalt loodud universumi panna oma andmeid sellele lõuendile saatma.

setLayout(new BorderLayout());

add(c, BorderLayout.CENTER);

määravad paigutushalduriks BorderLayout'i mille tulemusena õnnestub loodud lõuend paigutada rakendi (graafikakomponendi) keskele ning kuna sellesse rakendisse muid komponente paigutatud pole, siis venitatakse kolmemõõtmelise graafikakomponendi tarvis loodud lõuend üle kogu rakendile eraldatud pinna laiali.

BranchGroup juur = new BranchGroup();

loob hierarhia alguse, mille külge saan edasi kujundeid paigutada. Isendile annan nimeks juur, sest tegemist olekski nagu puu juurega.

juur.addChild(new ColorCube(0.5));

loob värvilise kuubi küljepikkusega 0,5 suhtelist pikkusühikut ning paigutab selle juure järglaseks (leheks).

juur.compile();

optimeerib loodud süsteemi. Ühe lihtsa komponendi puhul ei pruugi olulist kiirusevõitu olla, kuid vähegi rohkemate või keerulisemate kujundite puhul luuakse selle käsu tulemusena seosed, mille tulemusena saab pilti märgatavalt kiiremini ekraanile manada ning liigutada või valguse peegeldusi arvutada.

SimpleUniverse u = new SimpleUniverse(c);

tulemusena luuakse ruum (universum), mis oma sees paikneva vaataja asukohast paistva pildi saadab eelnevalt loodud lõuendile nimega c.

u.getViewingPlatform().setNominalViewingTransform();

nihutab vaataja veidi nullpunktist eemale, nii et keskele (vaikimisi asukoht) paigutatud oleksid nähtavad.

u.addBranchGraph(juur);

määrab kujunditepuu, millist loodud ruumis näitama hakatakse.

Edasised käsud on juba traditsioonilised, et loodud süsteem ka silmale nähtavaks teha. Kui rakend käivitada veebilehel, siis võib main-meetodi kõige täiega ära jätta. Sel juhul tuleks aga hoolitseda, et 3D oleks ka brauseri JRE juurde installeeritud (Netscape puhul Windows 95 all näiteks kataloogi C:\Program Files\Netscape\Communicator\Program\java).

Kuubi keeramine

Keeramise korral tuleb juure ning kuubi vahele paigutada keerav sõlm. Transform3D suudab nii nihutada kui keerata.

Transform3D keerd1=new Transform3D();

keerd1.rotX(Math.PI/4);

TransformGroup keere1=new TransformGroup(keerd1);

tulemusena loodakse sõlm (tüübist TransformGroup), mis panduna juure ja kuubi vahele keerab viimast nii palju kui sõlmes ette nähtud.

BranchGroup juur = new BranchGroup();

juur.addChild(keere1);

keere1.addChild(new ColorCube(0.5));

juur.compile();

Nagu analoogia põhjal oletada võib, on klassis Transform3D lisaks rotX-le kasutada ka meetodid rotY ning rotZ keeramiseks, lisaks transform() nihutamiseks ning matemaatikahuvilistele veel hulga vahendeid asukoha määramiseks. Kogu arvutamine käib – nagu pea mujalgi kolmemõõtmelises graafikas – maatriksite ja vektorite korrutamise abil.

Nihutamine

Keeramine ja nihutamine käivad sarnaselt. Mõlemal juhul tuleb muutuse andmed esialgu paigutada Transform3D tüüpi objekti ning seejärel sealtkaudu TransformGroup'ile üle kanda. Nihutamiseks on Transform3D-l käsk setTranslation, mis soovib parameetriks Vector3f-i, ehk andmeid nihke kohta iga telje suhtes.

BranchGroup juur = new BranchGroup();

Transform3D t3d1=new Transform3D();

t3d1.setTranslation(new Vector3f(0.5f, 0, 0));

TransformGroup tg1=new TransformGroup(t3d1);

juur.addChild(tg1);

tg1.addChild(new ColorCube(0.5));

juur.compile();

X-telg viib paremale, y üles ning z kasutaja poole. Täht f numbri taga tähendab, et tegemist on ühekordse täpsusega reaalarvuga (float).

Kui soovida nii nihutada kui keerata, siis tuleb need tegevused sooritada üksteise järel. Luuakse kaks TransformGroup'i ning pannakse nad üksteise järel hierarhiasse, nii et juur -> tg1(nihe) -> keere1 -> kuup. Selliselt järgnevate muunete omadused liituvad.

Transform3D t3d1=new Transform3D();

t3d1.setTranslation(new Vector3f(0.5f, 0, 0));

TransformGroup tg1=new TransformGroup(t3d1);

Transform3D keerd1=new Transform3D();

keerd1.rotX(Math.PI/4);

TransformGroup keere1=new TransformGroup(keerd1);

juur.addChild(tg1);

tg1.addChild(keere1);

keere1.addChild(new ColorCube(0.5));

juur.compile();

Sama tulemuse võib ka lühemalt saavutada, arvutades nii keeramise kui nihke summa välja ühe Transform3D objekti sees ning tulemus määrata ühe TransformGroup'i omaduseks.

Transform3D t3d1=new Transform3D();

t3d1.setTranslation(new Vector3f(0.5f, 0, 0));

Transform3D keerd1=new Transform3D();

keerd1.rotX(Math.PI/4);

t3d1.mul(keerd1);

TransformGroup tg1=new TransformGroup(t3d1);

juur.addChild(tg1);

tg1.addChild(new ColorCube(0.5));

juur.compile();

Käsk mul (multiple) korrutab kahe maatriksi väärtused (ühendab nendes paiknevad omadused) ning paneb tulemuse esimesse algse väärtuse asemel. Seda Transform3D'd saab nüüd kasutada kui algsete omaduste summat.

Liigutamine

Järgneva näite tulemusena pannakse kuup ekraanil keerlema ning lähemale-kaugemale nihkuma.

import java.awt.*;

import javax.swing.*;

import com.sun.j3d.utils.geometry.ColorCube;

import com.sun.j3d.utils.universe.SimpleUniverse;

import javax.media.j3d.*;

import javax.vecmath.*;

public class Kuup2a extends JApplet implements Runnable{

TransformGroup keere1;

double nurk;

public Kuup2a() {

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

getContentPane().add(c, BorderLayout.CENTER);

BranchGroup juur = new BranchGroup();

Transform3D keerd1=new Transform3D();

keere1=new TransformGroup(keerd1);

keere1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

juur.addChild(keere1);

keere1.addChild(new ColorCube(0.5));

juur.compile();

SimpleUniverse u = new SimpleUniverse(c);

u.getViewingPlatform().setNominalViewingTransform();

u.addBranchGraph(juur);

new Thread(this).start();

}

public void run(){

while(true){

try{Thread.sleep(50);}catch(Exception e){}

nurk+=0.1;

double kaugus=-1+Math.sin(nurk/3);

Transform3D t=new Transform3D();

t.rotX(nurk);

t.setTranslation(new Vector3d(0, 0, kaugus));

keere1.setTransform(t);

}

}

public static void main(String[] args) {

Frame f=new Frame("Keerlev kuup");

f.add(new Kuup2a());

f.setSize(300, 300);

f.setVisible(true);

}

}

Võrreldes eelmise näitega on objektipuu loomisel juures üks käsk

keere1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

mille tulemusena lubatakse muundusgrupi väärtusi ka programmi töö käigus muuta. Muutmine ise on toodud eraldi lõime, meetodisse run, kus igal sammul suurendatakse nurka 0.1 radiaani võrra ning vastavalt sellele määratakse kuubi keere ning nihe. Kui soovida, et kuup kaugust vaatajast ei muuda, siis võib kaugusega seotud käsud välja jätta. Samuti nagu siin run-käsus tsüklina kuupi keerates võib ka mujal mitmesugustele andmetele vastavalt. Nii võib rahumeeli paluda kujundeid paigutada vastavalt kasutaja sisestatud või võrgust saabunud andmetele.

Interpolaatorid

Liikumisi tuleb kolmemõõtmelises graafikas küllalt palju ette. Nende sujuvamaks loomiseks on kasutaja vabastatud pidevast lõimede kirjutamisest ning ta võib koostada interpolaatoreid, mis hoolitsevad muundusgrupi kasutajale sobiva oleku eest. Interpolaatori "südameks" on Alpha, mis vastavalt kasutaja poolt etteantud parameetritele muudab enese sees arvu väärtusega nulli ja ühe vahel. Interpolaator vaatab iga natukese aja tagant seda väärtust ning vastavalt sellele seab muundusgrupi parameetrid. RotationInterpolatori puhul vastab Alpha väärtusele 0-null ning 1-täisring, muud suurused vahepeal. Esimene parameeter tähendab korduste arvu (-1 vastab igavesele pöörlemisele), teine aega millisekundites, mille jooksul suureneb väärtus nullist üheni. Siinses näites siis pööreldakse igavesti, kulutades täisringile kümme sekundit. Kuna algseisu ning täisringi puhul on kuup samas asendis, siis paistabki liikumine ühtlane, kuigi vahepeal toimub muundegrupi väärtuses täisringine nihe, kui Alpha hüppab väärtuselt 1 järsku 0 peale tagasi. Interpolaator on siin näites pandud objektihierarhiasse ühes kuubiga lehena muundegrupi järglaseks. Viimane omakorda kuulub juure alla.

BranchGroup juur = new BranchGroup();

TransformGroup keere1=new TransformGroup();

keere1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

RotationInterpolator keeraja1=

new RotationInterpolator(new Alpha(-1, 10000), keere1);

keeraja1.setSchedulingBounds(new BoundingSphere());

juur.addChild(keere1);

keere1.addChild(keeraja1);

keere1.addChild(new ColorCube(0.5));

juur.compile();

Interpolaatoreid on mitmesuguseid. PositionInterpolator suudab kujundeid (või nende komplekti) liigutada kahe punkti vahel. Millisel ajahetkel ese kus paigas asub, seda määrab jällegi isend tüübist Alpha. Temagi muutumisi saab täpsemalt määrata. Parameetriteta konstruktori puhul kasvab väärtus sekundi jooksul nullist üheni ning siis asub jälle otsast peale. Põhjalikuma määramise puhul – nagu järgnevast näitest näha – on Alpha parameetrite järjekord selline:

1. korduste arv (-1=lõpmatus)

2. lubatud suunad(kasvamine/kahanemine)

3. ooteaeg enne käivitumist (kõik ajad millisekundites)

4. ooteaeg iga ringi algul, kasvamiskiiruse suurenemise aeg

5. üheni jõudmise aeg

6. väärtusel 1 püsimise aeg

7. vähenemiskiiruse suurenemise aeg

8. nullini jõudmise aeg

9. nullil püsimise aeg.

PositionInterpolatori konstroktoris määratakse ära Alpha, muundusgrupp muutmiseks, liikumissuund ning pikkused palju algasendist edasi ning tagasi liikuda. Liikumissuuna võib Transform3D abil keerata täpselt selliseks nagu vaja.

BranchGroup juur = new BranchGroup();

TransformGroup tg1=new TransformGroup();

tg1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

Transform3D suund=new Transform3D();

suund.rotZ(Math.PI/2); //keerab ümber z-telje

Alpha a=new Alpha(-1, Alpha.INCREASING_ENABLE | Alpha.DECREASING_ENABLE ,

0, 2000, 2000, 2000, 0, 2000, 2000, 0);

PositionInterpolator liigutaja1=

new PositionInterpolator(a, tg1, suund, -0.6f, 0.5f);

liigutaja1.setSchedulingBounds(new BoundingSphere());

juur.addChild(tg1);

tg1.addChild(liigutaja1);

tg1.addChild(new ColorCube(0.2));

juur.compile();

Sarnaselt töötab ScaleInterpolator, mille abil kujundi suurust muuta võib.

BranchGroup juur = new BranchGroup();

TransformGroup tg1=new TransformGroup();

tg1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

ScaleInterpolator ip1= new ScaleInterpolator(new Alpha(), tg1);

ip1.setSchedulingBounds(new BoundingSphere());

juur.addChild(tg1);

tg1.addChild(ip1);

tg1.addChild(new ColorCube(0.2));

juur.compile();

Liikumistrajektoori võib punktide kaupa ette anda. Selleks tuleb kirjeldada punktide asukohad ning ajad, millal mingis punktis peab olema. Aegade väärtused tuleb määrata järjest, nullist üheni (ka Alpha annab sama vahemiku) ning aegu peab olema sama palju kui punkte. Siin näites algab liikumine koordinaatide alguspunktist. Kui Alpha on jõudnud 0,7-ni selleks ajaks asub kuup punktis (1, 0, 0) ehk on liikunud ühe ühiku võrra paremale. Järgneva 0,3 Alpha-ühiku jooksul nihutatakse kuup diagonaalis vasakule üles, nii, et ajal kui Alpha=1, on kuup punktis (0, 1, 0). Siis jälle tuldud teed tagasi. Liikumistee võib ette arvutada hulga pikema, nii et saab koostatud kujundi päris keerukat rada pidi käima panna. Kui keeramisrealt (suund.rotZ(Math.PI/2)) kommentaarimärgid eest ära võtta, siis liigub kuup kõigepealt üles ning sealt vasakule alla, sest siis on kogu liikumistee ümber Z-telje täisnurga jagu vasakule pööratud.

TransformGroup tg1=new TransformGroup();

tg1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

Transform3D suund=new Transform3D();

// suund.rotZ(Math.PI/2); //keerab liikumistrajektoori ümber z-telje

Alpha a=new Alpha(-1, Alpha.INCREASING_ENABLE | Alpha.DECREASING_ENABLE ,

0, 2000, 2000, 2000, 0, 2000, 2000, 0);

float[] ajad={0, 0.7f, 1};

Point3f[] punktid={

new Point3f(0, 0, 0),

new Point3f(1, 0, 0),

new Point3f(0, 1, 0)

};

PositionPathInterpolator liigutaja1=

new PositionPathInterpolator(a, tg1, suund, ajad, punktid);

liigutaja1.setSchedulingBounds(new BoundingSphere());

juur.addChild(tg1);

tg1.addChild(liigutaja1);

tg1.addChild(new ColorCube(0.2));

Kaks kuupi

Esimesed näited olid koostatud ühe kuubiga vaid seepärast, et tulemus lihtsamini kätte tuleks ning kood lühem välja näeks. Täiesti samamoodi saab kujundeid ka juurde lisada. Kui need aga otse juure külge panna, siis satuvad nad otse üksteise peale/sisse ning mõni võib sootuks teise taha peitu jääda et teda sugugi näha ei ole. Kui aga vähemalt üks objekt eemale nihutada, siis on kummalgi oma koht ning neid võib rahumeeli ekraani peal vaadelda.

BranchGroup juur = new BranchGroup();

Transform3D tr1=new Transform3D();

tr1.rotX(Math.PI*2/3);

tr1.setTranslation(new Vector3d(0.5, 0, 0));

TransformGroup tg1=new TransformGroup(tr1);

juur.addChild(tg1);

tg1.addChild(new ColorCube(0.2));

juur.addChild(new ColorCube(0.1));

juur.compile();

Muud kujundid

Lisaks värvilisele kuubile, millega algul hea katseid teha, leiab geomeetriapaketist veel silindri (Cylinder), koonuse (Cone), risttahuka (Box) ning kera (Sphere). Neile pole veel värvi antud, seetõttu tuleb see töö ise ära teha.

Cylinder s1=new Cylinder(0.2f, 1.2f); //raadius, pikkus

s1.setAppearance(new Appearance());

juur.addChild(s1);

Nagu aimata võib, saab silindrile ette anda raadiuse ning kõrguse, koonusele samuti. Risttahukale kolme külje pikkused ning kerale raadiuse.

Taust

Soovides tagapinnaks oleva musta tausta millegi muu värvi vastu vahetada, tuleb lihtsalt kirjutada millist värvi selle asemele soovitakse. Ning nagu muud elemendid, tuleb seegi juure külge haakida.

Background taust=new Background(new Color3f(Color.yellow)); //kollane taust

taust.setApplicationBounds(new BoundingSphere(new Point3d(), 1000));

juur.addChild(taust);

Vaatekoha muutmine

Et ruumis ringi liikuda või lihtsalt pilti teise nurga alt vaadata, selleks võib oma vaateplatsi asukohta muuta. Järgmise paari reaga luuakse uus Transform3D, määratakse sellele parameetrid (0,6 ühikut üles, 3 ettepoole) ning palutakse vaataja silmad ehk kaamera selle koha peale paigutada. Kui ise liikuda ülespoole, siis paistab pilt selle jagu altpoolt.

Transform3D t=new Transform3D();

t.setTranslation(new Vector3f(0, 0.6f, 3));

u.getViewingPlatform().getViewPlatformTransform().setTransform(t);

Järgnevalt veidi pikem näide, kus lennutatake taevasse hulk kuupe juhuslikesse asukohtadesse tähtedeks ning seejärel võib oma asukohta muutes kui kosmoselaevaga mööda taevalaotust ringi liikuda. Iga kuubi tarvis luuakse oma muundegrupp ning selle abil nihutatakse kuup keskpunkti suhtes juhuslikult kuni +/- 50 ühiku võrra igas suunas. KeyNavigatorBehavior võimaldab vaateplatvormilt küsitud TransformGroupi muuta ning selle abil meile ruumis liikumis ette kujutada.

import java.applet.Applet;

import java.awt.*;

import com.sun.j3d.utils.geometry.ColorCube;

import com.sun.j3d.utils.universe.SimpleUniverse;

import com.sun.j3d.utils.behaviors.keyboard.*;

import javax.media.j3d.*;

import javax.vecmath.*;

public class Asukoht2 extends Applet {

public Asukoht2() {

setLayout(new BorderLayout());

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

add(c, BorderLayout.CENTER);

BranchGroup juur = new BranchGroup();

for(int i=1; i<1000; i++){ //luuakse hulk juhuslikke kuupe taevasse

Transform3D t3=new Transform3D();

t3.setTranslation(new Vector3f((float)(100*Math.random()-50),

(float)(100*Math.random()-50),

(float)(100*Math.random()-50)));

TransformGroup tg=new TransformGroup(t3);

tg.addChild(new ColorCube(0.4));

juur.addChild(tg);

}

SimpleUniverse u = new SimpleUniverse(c);

TransformGroup tg=u.getViewingPlatform().getViewPlatformTransform();

KeyNavigatorBehavior kb=new KeyNavigatorBehavior(tg);

kb.setSchedulingBounds(new BoundingSphere(new Point3d(), 1000));

juur.addChild(kb);

Transform3D t=new Transform3D(); //Määratakse vaatekoht

t.setTranslation(new Vector3f(0, 0, -5));

u.getViewingPlatform().getViewPlatformTransform().setTransform(t);

Background taust=new Background(new Color3f(Color.blue)); //sinine taust

taust.setApplicationBounds(new BoundingSphere(new Point3d(), 1000));

juur.addChild(taust);

juur.compile();

u.addBranchGraph(juur);

}

public static void main(String[] args) {

Frame f=new Frame("Kuubid taevas");

f.add(new Asukoht2());

f.setSize(300, 300);

f.setVisible(true);

}

}

Kiri

Lihtne kahemõõtmeline tekst õnnestub ekraanile manada küllalt kergesti.

juur.addChild(new Text2D("Tervitus", new Color3f(Color.green),

"Times", 55, Font.ITALIC));

Selle sama teksti pöörlema panek on aga natuke suurem ettevõtmine. Samas aga on tulemus küllaltki ilus ning mõnelgi juhul võib end ära tasuda. Endiselt tuleb lubada muundegrupi väärtust programmi töö ajal kirjutada, et saaksime teksti nurka muuta. Tagapoolsed ettevõtmised pinnaga hoolitsevad, et saaksime teksti mõlemat külge näha. Vaikimisi hoiab arvuti enese energiat kokku ning ei soostu kirja tagapoolt näitama.

TransformGroup keere1=new TransformGroup();

keere1.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);

RotationInterpolator keeraja1=

new RotationInterpolator(new Alpha(-1, 10000), keere1);

keeraja1.setSchedulingBounds(new BoundingSphere());

juur.addChild(keere1);

keere1.addChild(keeraja1);

Text2D tekst=new Text2D("Tervitus", new Color3f(Color.green),

"Times", 55, Font.ITALIC);

PolygonAttributes pind=new PolygonAttributes();

pind.setCullFace(PolygonAttributes.CULL_NONE); //et ka teine pool näha oleks

tekst.getAppearance().setPolygonAttributes(pind);

keere1.addChild(tekst);

juur.compile();

Ka kolmemõõtmelise kirja puhul tuleb hoolitseda, et seda ekraanil näitama soostutaks. Text3D iseenesest kirjeldab vaid kuju ehk geomeetria. Nägemiseks peab looma kujundi (Shape3D) ning seadma talle geomeetria ning materjali. Et materjal ruumis paistaks, selleks lubame seda valgustada (setLightingEnable) ning paigutame ruumi tausta/hajuvalguse allika. Nii ilmub õrn kolmemõõtmeline tekst ekraanile.

Text3D t=new Text3D(

new Font3D(new Font("Helvetica", Font.PLAIN, 1), new FontExtrusion()),

"Tere" , new Point3f(-1, 0.6f, -1.5f)

);

Material m=new Material(); m.setLightingEnable(true);

Appearance a=new Appearance(); a.setMaterial(m);

Shape3D s=new Shape3D();

s.setGeometry(t); s.setAppearance(a);

juur.addChild(s);

Color3f valgusvarv=new Color3f(Color.white);

AmbientLight al=new AmbientLight(valgusvarv);

al.setInfluencingBounds(new BoundingSphere());

juur.addChild(al);

juur.compile();

Tasapind

Omale sobivatest tasapindadest saab kokku ehitada kõik meile sobivad kujundid. Ka kera pole siinse programmi jaoks muud kui piisavalt tihedasti üksteise kõrvale pandud kolmnurkade kogum. QuadArray abil saab määrata loodava pinna nurgad ning siis paluda nende vahele pind koostada. Edasine toiming sama kui kolmemõõtmelise teksti puhul: geomeetria ja materjal ühendada kujundiks ning selle nägemiseks panna ta lavagraafi(puusse) ja lasta valgus peale.

QuadArray nurgad=new QuadArray(4, GeometryArray.COORDINATES

| GeometryArray.COLOR_3 | GeometryArray.NORMALS);

nurgad.setCoordinate(0, new Point3f(-0.5f, 0, 0));

nurgad.setCoordinate(1, new Point3f( 0.5f, 0, 0));

nurgad.setCoordinate(2, new Point3f( 0, 0.2f, 0));

nurgad.setCoordinate(3, new Point3f( 0, 0.4f, 0));

Shape3D kujund=new Shape3D();

kujund.setGeometry(nurgad);

Appearance a=new Appearance();

a.setMaterial(new Material());

kujund.setAppearance(a);

juur.addChild(kujund);

AmbientLight taustavalgus=new AmbientLight();

taustavalgus.setInfluencingBounds(new BoundingSphere());

juur.addChild(taustavalgus);

juur.compile();

Joonemassiiv

Nii pindadest kui joontest võib oma tarbeks kujundi luua. Järgnevas näites luuakse kahest joonest L-täht mida võib edaspidi kasutada nii nagu tavalist kujundit, nagu näiteks kuupi või koonust.

import javax.media.j3d.*;

import javax.vecmath.*;

public class SuurL extends Shape3D{

Point3d p1=new Point3d(0, 0, 0),

p2=new Point3d(0, 1, 0),

p3=new Point3d(0.5, 0, 0);

Point3d[] jooned={

p1, p2,

p1, p3

};

public SuurL(){

LineArray joonemassiiv=new LineArray(4, LineArray.COORDINATES);

joonemassiiv.setCoordinates(0, jooned);

setGeometry(joonemassiiv);

setAppearance(new Appearance());

}

}

Selline klass tuleb salvestada eraldi faili ning edaspidi kui tarvist seda kasutada, tuleb hoolitseda, et see SuurL asuks samas kataloogis või sisseloetavas paketis ning loodud tähe ekraanile manamiseks piisab vaid käsust

juur.addChild(new SuurL());

Valgus

Vaid osa kujundeid suudame näha siis, kui neile valgus peale ei paista. Ka ülejäänuid on võimalik pealelangeva valgusega ilmestada. Java3D on loodud liikuvate kujundite tarbeks ning värvipeensuste arvutamiseks kuigi palju aega ei kulutata, sellegipoolest võib hea tahtmise korral täiesti äratuntava pildi ekraanile manada. Fotokvaliteediga ühe pildi algandmetest välja arvutamiseks kulub võimsatel arvutitel tunde ning siiski tuleb osa tegelikkuses aset leidvaid peegeldumisi ja muid seoseid tähelepanuta jätta.

Java3D abil saab esitada haju-, suund-, punkt- ning kohtvalgust. Esimene on nagu päevavalgus, see on hajunud ühtlaselt üle ruumi ning selle abil on võimalik ka laua all ning kapi taga esemeid näha. Suundvalguse kiired on paralleelsed, samuti nagu need mis päikeselt meieni jõuavad. Punktvalgus levib ühest punktist alates igas suunas laiali. Kohtvalguse puhul saab lisaks määrata ruuminurga, kui laia koonusena see valgus laiali läheb.

Valgustatavatel kehadel peavad olema välja arvutatud pinnanormaalid. Isegi pealtnäha kumerad pinnad on arvuti tarvis pisikeste kolmnurgakujuliste tasapindade ühendid, kus iga tasapinna jaoks vastavalt valgustatusele tema värv välja näidatakse. Nagu muud 3D objektid, tuleb ka valgus lisada elementide puusse ning määrata tema mõjupiirkond (InfluencingBounds).

BranchGroup juur = new BranchGroup();

Appearance a=new Appearance();

a.setMaterial(new Material());

juur.addChild(new Sphere(0.5f, Sphere.GENERATE_NORMALS, a));

AmbientLight taustavalgus=new AmbientLight();

taustavalgus.setInfluencingBounds(new BoundingSphere());

juur.addChild(taustavalgus);

Suundvalguse lisamine on peaaegu analoogiline

BranchGroup juur = new BranchGroup();

Appearance a=new Appearance();

a.setMaterial(new Material());

juur.addChild(new Sphere(0.5f, Sphere.GENERATE_NORMALS, a));

DirectionalLight suundvalgus=new DirectionalLight();

suundvalgus.setInfluencingBounds(new BoundingSphere());

juur.addChild(suundvalgus);

juur.compile();

Punktvalguse puhul esimene punkt näitab valgusallika asukohta, teine valguse nõrgenemist. Valgustatus mingis punktis arvutatakse valemi järgi 1/(k1+kaugus*k2+kaugus*kaugus*k3), kus k1-k3 on teise Point3f-i parameetriteks antavad väärtused. Nii, et esimene vähendab heledust igal poole, teine võrdeliselt kaugusega ning kolmas võrdeliselt kauguse ruuduga.

PointLight punktvalgus=new PointLight(

new Color3f(Color.green), new Point3f(-0.6f, -0.7f, 0), new Point3f(0, 0, 1)

);

punktvalgus.setInfluencingBounds(new BoundingSphere());

juur.addChild(punktvalgus);

Kohtvalguse puhul antakse lisaks punktvalgusele ka suund (vektori abil) ja nurk, kui laialt valgus paistab. Viimane parameeter näitab, kui palju on sõõri keskus enam valgustatud kui ääred. Kui see väärtus on 0, siis paistab valgus ühtlaselt igale poole.

SpotLight kohtvalgus=new SpotLight(

new Color3f(Color.green), new Point3f(-0.5f, -0.7f, 0), new Point3f(0, 0, 1),

new Vector3f(1, 1, 0), (float)Math.PI/8, 0.5f

);

kohtvalgus.setInfluencingBounds(new BoundingSphere());

juur.addChild(kohtvalgus);

Materjal

Kujundite pindade omadusi määratakse materjali abil. Kui materjal või muul moel väljanägemine puudub, siis pole ka midagi näha. Eralduva valguse abil määratakse värv, mis paistab ka siis, kus keha peale muud valgust ei tule. Selliselt on määratud näiteks värvilise kuubi küljed, millega eespool mitmel pool tutvusime. Koonus ja silinder vaikimisi ei helenda, nende nägemiseks tuleb sinna kas valgus peale suunata või neile endile värvus määrata. Allpool määratakse koonuse helenduv valgus roheliseks ning seetõttu näemegi seda ekraanil rohelisena.

BranchGroup juur = new BranchGroup();

Cone k1=new Cone();

Appearance valimus=new Appearance();

Material materjal=new Material(

new Color3f(Color.black), //hajuvalgus

new Color3f(Color.green), //eralduv

new Color3f(Color.green), //peegelduv valgus

new Color3f(Color.black), 1 //läige

);

valimus.setMaterial(materjal);

k1.setAppearance(valimus);

juur.addChild(k1);

juur.compile();

Muster

Lisaks ühtlasele värvile või mitme valguse üheaegsest pealepaistmisest tingitud värviüleminekule võib keha pinnaks määrata mustri. Arvutuskiiruse suurendamiseks peavad mustriks määratud pildi laius ja kõrgus punktides olema arvu 2 astmed, ehk 2, 4, 8, 16 jne. Mõne kujundi (näiteks tasapind) puhul on lisaks vaikemäärangutele võimalik mustripilti ka mitmeti kujundi peale seada: keerata väänata, võtta sellest vaid osa jne.

BranchGroup juur = new BranchGroup();

Appearance a=new Appearance();

TextureLoader mustrilugeja=new TextureLoader("taust1.gif", this);

ImageComponent2D pilt=mustrilugeja.getImage();

Texture2D muster = new Texture2D(Texture.BASE_LEVEL, Texture.RGBA,

pilt.getWidth(), pilt.getHeight());

muster.setImage(0, pilt);

a.setTexture(muster);

juur.addChild(new Sphere(0.5f, Primitive.GENERATE_TEXTURE_COORDS, a));

juur.compile();

Töö käigus kujundite lisamine

Pärast programmi algset käivitamist saab kujundeid lisada vaid koos uue oksa ehk BrahchGroupiga. Sedagi vaid juhul, kui algsele juurele on lisatud omadus ALLOW_CHILDREN_WRITE, ehk maakeeli öelduna tohib siis sinna järglasi juurde panna (või ära võtta). Nii ka siin all olevas näites nupule vajutamise puhul luuakse kõigepealt uus BranchGroup, selle külge lisatakse kujund (kuup). Siis oksa näitamine optimeeritakse (compile) ning alles seejärel lisatake oks olemasoleva juure külge. Kui kõik ilusti töötab, siis on nupu vajutamise peale näha, kuidas kuubi esikülg nupuvajutuse peale ekraanile juurde tekib.

Lisada võib ka suuremat kujundite gruppi. Siis tuleb see lihtsalt enne ekraanile paigaldamist valmis teha ning alles siis üheskoos sinna paigutada. Kui soovida lisada mujale kui keskkohta (mis on ju täiesti loomulik soov), siis peab oksa ja esemete vahele paigutama (vähemalt ühe) TransformGroup'i, mille abil siis kujund sobivasse asupaika nihutada ning keerata.

import java.awt.*;

import java.awt.event.*;

import javax.swing.*;

import com.sun.j3d.utils.geometry.*;

import com.sun.j3d.utils.universe.SimpleUniverse;

import javax.media.j3d.*;

import javax.vecmath.*;

public class Kuubilisamine1a extends JApplet implements ActionListener{

TransformGroup keere1;

Button nupp=new Button("Lisa kuup");

BranchGroup juur = new BranchGroup();

public Kuubilisamine1a() {

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

getContentPane().add(c, BorderLayout.CENTER);

getContentPane().add(nupp, BorderLayout.NORTH);

juur.setCapability(TransformGroup.ALLOW_CHILDREN_WRITE);

juur.compile();

SimpleUniverse u = new SimpleUniverse(c);

u.getViewingPlatform().setNominalViewingTransform();

u.addBranchGraph(juur);

nupp.addActionListener(this);

}

public void actionPerformed(ActionEvent e){

BranchGroup oks1=new BranchGroup();

oks1.insertChild(new ColorCube(0.3), 0);

oks1.compile();

juur.insertChild(oks1, 0);

}

}

Ruumimängu põhi

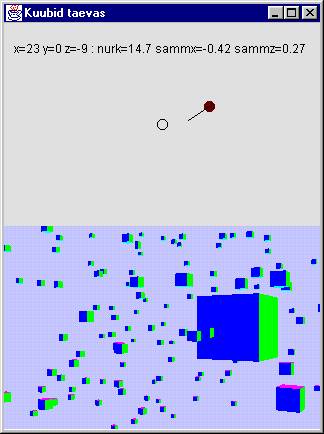
Järgneval paaril leheküljel oleva näite järgi saab ehitada mitmeid kolmemõõtmelisi mänge – ja miks mitte ka asjalikke tutvustavaid programme, muutes väljanägemist, lisades kaunimaid ja keerukamaid kujundeid, määrates lubatud ja lubamatu liikumise piirkondi ning vajaduse korral andmeid võrgu kaudu teise kasutajani saates ja sealt teispoole teateid arvesse võttes. Samu sündmusi on näha kahel pinnal. Alumises saab kasutaja klahvide abil muuta oma asukohta ruumis, nähes, kuidas tähtedeks olevad kuubikesed tema silmade läbi paistavad. Üleval on näha tema asukohta määravad parameetrid, samuti tasandil kujutadud pinnal kasutaja asukoht ning vaatesuund universumis ning viimase keskkoht. See peaks aitama jälgida enese asukohta ning vältima eksimisi, mis kosmoses ilma vaatlusandmeteta ringi hõljudes on küllalt kerge tulema.

Peaklassi sisse on loodud kaks sisemist klassi, üks klahvivajutustele reageerimiseks ja liikumise eest hoolitsemiseks, teine ülemisel tasapinnalisel lõuendil kasutaja andmete näitamiseks. Kõikjal vajaminevad andmed kasutaja asukoha ja suuna kohta kirjeldati peaklassi alguses, nii on need kergesti kõikjale kätte saadavad ning vajaduse korral on ka näiteks võrgu kaudu andmete vahetamist lihtne korraldada.

Nooleklahvid "Üles" ja "Alla" liigutavad kasutajat edasi-tagasi vastavalt tema vaatesuunale. Teiste nooleklahvidega saab vaatesuunda vastavalt kas paremale või vasakule pöörata. Enese püstloodis kõrgemale või madalamale nihutamiseks aitavad leheküljeklahvid "Page up" ning "Page down", viltusuunas nihutamiseks lihtuse mõttes vahendeid loodud ei ole. Kuna aga asukohta saab kergesti muutujate väärtuste abil määrata, siis on sellise võimaluse lisamine täiesti võimalik. Praeguse lähenemise juures on kergemini võimalik piirduda kahemõõtmelises ruumis kehtivate matemaatiliste valemitega, muul juhul tuleb kas programmi pikemaks või valemeid keerukamaks ajada.

import java.applet.Applet;

import java.awt.*;

import java.awt.event.*;

import com.sun.j3d.utils.geometry.ColorCube;

import com.sun.j3d.utils.universe.SimpleUniverse;

import com.sun.j3d.utils.behaviors.keyboard.*;

import javax.media.j3d.*;

import javax.vecmath.*;

public class Asukoht3a extends Applet {

float x, y, z, uusx, uusy, uusz,

nurk=0f, sammx, sammz, samm=-0.5f, nurgavahe=0.05f;

//samm on negatiivne, kuna silmad on z-teljel miinuse poole.

Canvas3D c = new Canvas3D(SimpleUniverse.getPreferredConfiguration());

SimpleUniverse u = new SimpleUniverse(c);

TransformGroup tg=u.getViewingPlatform().getViewPlatformTransform();

Canvas tasapind=new Plaan();

Klahvikuular k=new Klahvikuular();

public Asukoht3a() {

setLayout(new BorderLayout());

setLayout(new GridLayout(2, 1));

add(tasapind);

add(c);

BranchGroup juur = new BranchGroup();

for(int i=1; i<1000; i++){

Transform3D t3=new Transform3D();

t3.setTranslation(new Vector3f((float)(60*Math.random()-30),

(float)(60*Math.random()-30),

(float)(60*Math.random()-30)));

TransformGroup tg=new TransformGroup(t3);

tg.addChild(new ColorCube(0.3));

juur.addChild(tg);

}

juur.addChild(new ColorCube(2)); //suur kuup keskele

c.addKeyListener(k);

Background taust=new Background(new Color3f(new Color(200, 200, 255)));

taust.setApplicationBounds(new BoundingSphere(new Point3d(), 1000));

juur.addChild(taust);

u.addBranchGraph(juur);

tasapind.addFocusListener(new FocusListener(){

public void focusGained(FocusEvent e){c.requestFocus();}

public void focusLost(FocusEvent e){}

}); //hoolitksetakse, et klahvidele reageeriv ruumilõuend saaks fookusesse.

}

double umarda(double arv, double koht){

return Math.round(arv*Math.pow(10, koht))/Math.pow(10, koht);

}

public static void main(String[] args) {

Frame f=new Frame("Kuubid taevas");

f.add(new Asukoht3a());

f.setSize(400, 600);

f.setVisible(true);

}

class Klahvikuular implements KeyListener{

public Klahvikuular(){

arvutaSamm();

}

void arvutaSamm(){

sammz=(float)(Math.cos(nurk)*samm);

sammx=(float)(Math.sin(nurk)*samm);

}

public void keyPressed(KeyEvent e){

int klahv=e.getKeyCode();

if(klahv==KeyEvent.VK_RIGHT){ //keerab paremale

nurk-=nurgavahe;

arvutaSamm();

}

if(klahv==KeyEvent.VK_LEFT){

nurk+=nurgavahe;

arvutaSamm();

}

if(klahv==KeyEvent.VK_UP){ //edasi

uusx+=sammx;

uusz+=sammz;

}

if(klahv==KeyEvent.VK_DOWN){

uusx-=sammx;

uusz-=sammz;

}

if(klahv==KeyEvent.VK_PAGE_UP)uusy=y-samm; //üles

if(klahv==KeyEvent.VK_PAGE_DOWN)uusy=y+samm;

prooviAstuda();

}

void prooviAstuda(){

if(kasAsukohtSobib()){

omista();

liiguta();

tasapind.repaint();

} else {

piiksu();

}

}

/**

* Meetodi abil määratakse, kas uude arvutatud asukohta tohib kasutaja liikuda.

*/

boolean kasAsukohtSobib(){

if(uusy<10) return true;

else return false;

}

void omista(){

x=uusx;

y=uusy;

z=uusz;

}

void liiguta(){

Transform3D t1=new Transform3D();

Transform3D t2=new Transform3D();

t1.set(new Vector3d(x, y, z));

t2.rotY(nurk);

t1.mul(t2);

tg.setTransform(t1);

}

void piiksu(){

Toolkit.getDefaultToolkit().beep();

}

public void keyReleased(KeyEvent e){}

public void keyTyped(KeyEvent e){}

}

class Plaan extends Canvas{

public void paint(Graphics g){

g.setColor(new Color(230, 230, 230));

g.fillRect(0, 0, getWidth(), getHeight());

int keskx=getWidth()/2;

int kesky=getHeight()/2;

int varv=100+(int)(10*y); //vastavalt kõrgusele arvutatakse värv

if(varv<10)varv=10;

if(varv>240)varv=240;

g.setColor(new Color(varv, 0, 0));

g.fillOval(keskx+(int)(2*x)-5, kesky+(int)(2*z)-5, 10, 10);

g.setColor(Color.black);

g.drawString("x="+(int)x+" y="+(int)y+" z="+(int)z+" : nurk="+umarda(nurk, 2)+

" sammx="+umarda(sammx, 2)+" sammz="+umarda(sammz, 2) , 10, 30);

//koordinaate kirjeldav tekst

g.drawLine(

keskx+(int)(2*x), kesky+(int)(2*z),

keskx+(int)(2*x+50*sammx), kesky+(int)(2*z+50*sammz)

);

g.drawOval(keskx-5, kesky-5, 10, 10);

}

public void update(Graphics g){paint(g);}

}

}

Tehniline seletus

Import-käsklused on tuttavad eelsmistest näidetest ning täiesti tavalised. java.awt.event.* on siin tarvilik klahvivajutuste registreerimiseks. Canvas3D võimaldab neid kinni püüda ja vastu võtta nagu iga teinegi tavaline graafikakomponent.

float x, y, z, uusx, uusy, uusz,

nurk=0f, sammx, sammz, samm=-0.5f, nurgavahe=0.05f;

Muutujad x, y ja z tähistavad kasutaja parasjagu kehtivat asukohta, nurk vaatenurga muutust võrreldes lähteasendiga (pilk sihitud kaugusse mööda miinusesse eemalduvat z-telge); uusx, uusy ja uusz tähistavad kasutaja uut väljaarvutatud asukohta, enne kui viimane sinna liikunud on. Niimoodi on kergesti võimalik kontrollida, kas uude kohta ta üldse liikuda tohib, samuti, kas enne uude kohta jõudmist tuleb mõni eelnev operatsioon teostada (nt. uks avada või meloodialõik mängida). samm tähistab iga üksiku sammu pikkust ruumis. Negatiivne on ta seetõttu, et algasendis on silmad z-telje miinuspoolele suunatud ning edasi astudes paratamatult koordinaadi väärtus väheneb. Nurgavahe näitab, kui palju tuleb igal keeramisnupule vajutamisel vaatesuunda radiaanides muuta. Sammx ja sammz arvutatakse iga keeramise korral välja, et oleks teada, palju edasi või tagasi liikumise puhul vastavaid koordinaate muuta tuleb. Suurused on float tüüpi ehk ühekordse (mitte topelt) täpsusega reaalarvud, kuna Java3D on loodud enam liikumise tarvis ning siin arvestatakse enam sujuvust kui täpsust. float võtab arvutamisel vähem ressursse ning arvutamisest tekkivad erinevused pole siinse mõõtkava juures nagunii märgatavad.

TransformGroup tg=u.getViewingPlatform().getViewPlatformTransform();

Canvas tasapind=new Plaan();

Klahvikuular k=new Klahvikuular();

Kirjeldatud muutujate otstarve on järgmine:

tg tähistab kasutaja asukohta määravat TransformGroup'i. Selle omadusi muutes saab kasutajat nihutada ja keerata. Tasapinnal on näha andmed kasutaja asukohta ning klahvikuular hoolitseb selle määramise eest vastavalt vajutatud klahvidele.

for(int i=1; i<1000; i++){

Transform3D t3=new Transform3D();

t3.setTranslation(new Vector3f((float)(60*Math.random()-30),

(float)(60*Math.random()-30),

(float)(60*Math.random()-30)));

TransformGroup tg=new TransformGroup(t3);

tg.addChild(new ColorCube(0.3));

juur.addChild(tg);

}

juur.addChild(new ColorCube(2)); //suur kuup keskele

Tähtedeks olevatele kuupidele arvutatakse igal korral uus koht. Nii x-, y- kui z-telje peal leitakse igale koordinaadi väärtusele vastama juhuslik arv –30 ning 30 vahel. Seda teeb (60*Math.random()-30) , mis loob juhuarvu vahemikust 0..1, korrutab selle 60-ga (vahemik 0..60) ning lahutab tulemusest 30. Sulgudes (float) võrrandi ees muudab tüübi ühekordse täpsusega reaalarvuks, et tulemus muude siin kasutatavate andmetega kokku käiks. Allpool lisatud suur kuup aitab suures tähemeres orienteeruda ning näitab ekslemisel kätte nullpunkti asukoha.

tasapind.addFocusListener(new FocusListener(){

public void focusGained(FocusEvent e){c.requestFocus();}

public void focusLost(FocusEvent e){}

}); //hoolitksetakse, et klahvidele reageeriv ruumilõuend saaks fookusesse.

Asukoha klahvidega liigutamiseks on vajalik, et vajutusi registreeriv komponent oleks fookuses. Siin näites võib aktiivseks osutuda nii ülemine kui alumine graafikakomponent. Esimesel juhul aga teated kuularini ei jõua ning tulemusena võib kasutaja nuppe muudkui vajutada ja vajutada, aga soovitud liikumistulemust ei ole. Lisatud kuulari puhul saadab tasapind koheselt omale fookuse vastuvõtmise puhul selle edasi alumisele kolmemõõtmelisele lõuendile, niimoodi ei lähe kasutaja teated kaotsi. Sarnase tulemuse võiks saada, kui paneksime ka ülemise tasapinna samale klahvikuularile teateid saatma. Viimasel on ükskõik kust teated tulevad, tema ülesandes on neile vastavalt reageerida. Samuti võib ülemisel lõuendil fookuse vastuvõtmise lihtsalt ära keelata, tulemus oleks ikka sama. Niimoodi sisemise klassina loodud fookusekuular suudab alumise lõuendi poole pöörduda kuna viimane on loodud isendimuutujana. Alamprogrammis loodud muutujate puhul on selline lähenemine raskem.

double umarda(double arv, double koht){

return Math.round(arv*Math.pow(10, koht))/Math.pow(10, koht);

}

on lihtsalt abifunktsioon, kus etteantud arv ümardatakse etteantud kohtadeni pärast koma. Ta pole sisuliselt kuidagi siinse programmiga seotud, kuid aitab andmete välja kirjutamisel koodi lühendada. Lahtiseletatult: Math.pow(10, koht) leiab arvu 10 sellise astme, mida koht näitab. Kui koht on 2, siis selle avaldise tulemuseks on 100. Edasi korrutatakse arv leitud väärtusega läbi ning ümardatakse. Kui arv oli enne 0,657, siis nüüd on tulemuseks 66. Et taas algsesse vahemikku tagasi jõuda, tuleb uuesti tulemus leitud kümne astmega jagada.

public Klahvikuular(){

arvutaSamm();

}

void arvutaSamm(){

sammz=(float)(Math.cos(nurk)*samm);

sammx=(float)(Math.sin(nurk)*samm);

}

Nii klahvikuulari loomisel kui igakordsel vaataja suuna muutmisel palutakse tema nii x- kui z-koordinaadi suunas tehtava sammu pikkus uuesti välja arvutada. Siis saab edasi või tagasi liikumisel rahulikult neid väärtusi koordinaatidele lisada või eemadada, ilma, et peaks energiamahukat siinuse või koosiinuse arvutamist ette võtma. Nagu koolimatemaatikast teada, on koosinus sirge projektsioon ühe ning siinus teise koordinaattelje peal ehk täisnurkse kolmnurga peal vaadatuna lähis- ning vastaskülg.

public void keyPressed(KeyEvent e){

int klahv=e.getKeyCode();

if(klahv==KeyEvent.VK_RIGHT){ //keerab paremale

nurk-=nurgavahe;

arvutaSamm();

}

if(klahv==KeyEvent.VK_UP){ //edasi

uusx+=sammx;

uusz+=sammz;

}

Olles kasutajalt kinni püüdnud klahvivajutuse (meetod keyPressed käivitus), küsitakse sealt parameetrist edasise mugavama kasutuse huvides välja allavajutatud klahvi kood. Asutakse võrdlema, millist klahvi vajutati ning vastavalt sellele tegutsetakse edasi. Kui klahviks oli "Nool paremale", siis selle tulemusena vähendatakse nurga väärtust nurgavahe võrra ning arvutatakse välja uus samm liikumiseks nii x- kui z suunas. Paremale pööramisel tuleb lahutada seetõttu, et koordinaatteljestikul nurga suurenedes keeratakse vastupäeva, paremale poole saamiseks aga tuleb pöörata päripäeva.

if(klahv==KeyEvent.VK_PAGE_UP)uusy=y-samm; //üles

Üles liikumisel jäävad x- ning z-koordinaat muutmata, vaid y muutub ning seda siis terve sammupikkuse ulatuses.

prooviAstuda();

}

void prooviAstuda(){

if(kasAsukohtSobib()){

omista();

liiguta();

tasapind.repaint();

} else {

piiksu();

}

}

boolean kasAsukohtSobib(){

if(uusy<10) return true;

else return false;

}

Klahvivajutuskontrolli lõpuks kutsutakse välja meetod prooviAstuda(), kus otsustatakse, mida uute arvutatud koordinaatidega edasi tegema hakata. Tingimuses kasAsukohtSobib(), kontrollitakse, kas uutele arvutatud koordinaatidele tohib liikuda. Siin näites on tingimus lihtne, kasutajal ei lubata vaid tõusta kümne ja enama ühiku kõrgusele. Keerukamatel juhtudes saab aga siin hoolitseda selle eest, et kasutaja kõnniks ilusti mööda koridore, läbiks etteantud kontrollpunkti või ei jõuaks teisele liiklejale liiga lähedale.

Kui leiti, et uus asukoht sobib, siis omistatakse väljaarvutatud koordinaadid keha õigeteks koordinaatideks, liigutatakse ekraanil kasutaja sinna kohta ning samuti palutakse tasapind üle joonistada, et seal kasutaja kohta õiged andmed näha oleksid. Kui püüti liikuda keelatud kohale, siis selles näites tehakse sel puhul piiksu.

void liiguta(){

Transform3D t1=new Transform3D();

Transform3D t2=new Transform3D();

t1.set(new Vector3d(x, y, z));

t2.rotY(nurk);

t1.mul(t2);

tg.setTransform(t1);

}

Liigutamise tarvis arvutatakse nii nihke kui pööramise tarvis Transform3D. Nende omadused ühendatakse maatriksite korrutamise abil ning tulemus määratakse kasutaja asendiks.

class Plaan extends Canvas{

public void paint(Graphics g){

g.setColor(new Color(230, 230, 230));

g.fillRect(0, 0, getWidth(), getHeight());

Üleval paiknev andmelõuend kaetakse joonistuskäsu väljakutsel kõigepealt etteantud hallika värviga kogu oma suuruses. All olev update-meetodist otse paint'i väljakutse tähendab, et ekraani vahepealset lisapuhastust ei toimu. Sama tulemuse võiks isegi veidi vähemate koodiridadega saavutada, kui määrata lõuendi taustavärviks kohe hallikas. Sel juhul update hoolitseb enne joonistuse algust vana pildi mustriga katmise eest.

int keskx=getWidth()/2;

int kesky=getHeight()/2;

Edaspidise joonistamise tarbeks küsitakse lõuendilt keskkoht. Sellisel juhul jääb ruumi keskpunkt lõuendi keskele ka juhul, kui kasutaja viimase suurust peaks muutma.

int varv=100+(int)(10*y); //vastavalt kõrgusele arvutatakse värv

if(varv<10)varv=10;

if(varv>240)varv=240;

g.setColor(new Color(varv, 0, 0));

Kasutajat tähistava ringi värvus sõltub kasutaja asukoha kõrgusest. Mida kõrgemal see on, seda punasemalt joonistatakse kasutaja. Samas hoolitsetakse, et värvi määravate muutujate väärtused ei satuks äärmustesse, hoitakse, et punast värvi tähistav komponent oleks 10 ja 240 vahel. Kui 0 ja 255 vahelt väljuda, siis satutaks väärtusteni, mida pole võimalik ekraanil näidata ning väljastataks veateade.

g.fillOval(keskx+(int)(2*x)-5, kesky+(int)(2*z)-5, 10, 10);

Joonistatakse, arvestades koordinaate lõuendi keskpunktist. Kuna ovaali joonistamisel tuleb määrata vasak serv, siin aga soovime ringi keskpunkti panna kasutaja asukohta tähistama, tuleb 10 punkti laiuse ovaali sobivasse paika loomiseks selle vasak serv viie punkti võrra vasemale nihutada.

g.setColor(Color.black);

g.drawString("x="+(int)x+" y="+(int)y+" z="+(int)z+" : nurk="+umarda(nurk, 2)+

" sammx="+umarda(sammx, 2)+" sammz="+umarda(sammz, 2) , 10, 30);

//koordinaate kirjeldav tekst

Kasutaja vaatesuunda näitav joon algab ta asukohast lõuendil ning lõpeb sinna suunas, kuhu kasutaja vaadata ja liikuda saab. Algots lõuendil sõltub niisiis lõuendi keskpunktist ja kasutaja asukohast, lõppotsa puhul aga tuleb juurde veel vaatenurgast sõltuvad väärtused. Meie õnneks on x- ning z-suunalised sammud juba välja arvutatud, piisab vaid need piisavalt suure teguriga korrutada, et need ekraanil mõistlikena välja paistaksid.

g.drawLine(

keskx+(int)(2*x), kesky+(int)(2*z),

keskx+(int)(2*x+50*sammx), kesky+(int)(2*z+50*sammz)

);

g.drawOval(keskx-5, kesky-5, 10, 10);

}

public void update(Graphics g){paint(g);}

}

Kokkuvõte

Java3D abil õnnestub luua ruumiline keskkond, kontrollida ja muuta seal nii esemete kui kasutaja asukohta ja asendit. Piltide ja sissetoodud objektide abil õnnestub sealne keskkond piisavalt tõeliseks, et võiks võiks võrreldavalt muude 3D vahenditega tunda end virtuaalkeskkonna osana. Kõik kasutatavad vahendid peavad olema ühtses andmepuus. Leiduvad vahendid nihutamiseks ja keeramiseks (TransformGroup), automaatseks asukoha ning omaduste muutmiseks (Interpolaatorid) ning sündmuste peale käitumiseks (Behavior).

Ülesandeid

3D kujundid

· Loo ekraanile mitmesse kohta mitmesuguseid kuupe

· Koosta õu laternapostide, istepinkide, põrkava palli ning liigutatava palliga. Luba kasutajal oma asukohta muuta. Katseta värve, mustreid ja interpolaatoreid.

· Anna palli koordinaadid ette tekstiväljast.

3D võrgumäng

· Mängijate asukohad määratakse serverist tulevate andmete järgi. Samaaegselt on seis näha nii kahe- kui kolmemõõtmelisel kujul.

· Platsil on sein. Serveris olevate arvutuste järgi hoolitsetakse, et seda ei saaks läbida.

· Kujunda eelnenu põhjal võimalikult tõelisena näiv võrgumäng.