Rekursiivne joonistamine
Kordused, rekursiooni baas, fraktal
Plaan plaani peal
Ühe pargi keskel olnud
plaan, kuhu see park ilusti üles joonistatud. Kõik puud ja teed olnud ilusti
peal, samuti omal ka pargi plaan. Küll väiksemalt ja lihtsamalt, kuid siiski
võis tähtsamaid teid ja ojasid täiesti ära tunda. Ning pisikese täpina oli
sealgi näidatud plaani asukoht pargis. Nõndaviisi on see kui pildi sisse minek.
Samasugust nähtust võib tähele panna, kui kaameramees filmib ning filmi peale
jääb muu hulgas ka ekraan, kus parasjagu salvestatavat materjali näidatakse.
Nii satub tekkinud pilt üha uuesti ja uuesti ringlema ning vaatajale tundub
nagu ta saaks jälgida pikka koridori, kus avaneksid üha järgmised ja järgmised
uksed ning kõigis neis oleks üks ja sama sisu. Iga korraga ainult üha
väiksemalt ja väiksemalt, kuni meie silm või aparaadi eraldusvõime neid enam
üksteisest eraldada ei suuda. Samasuguse tulemuse võib saada ka lihtsamate
koduste vahenditega, kui üksteise vastu asendada kaks peeglit. Kumbki näitab teisele
saabuvat pilti tagasi ning tekkiv koridor võib välgukiirusel väga pikaks
kasvada. Olen näinud mitutteist peeglit üksteise seest paistmas ning see polnud
kindlasti mitte veel võimaluste tipp. Paremate peeglite, suurema valgustuse
ning põhjalikuma katsetamise juures saanuks tekkiva koridori pikkust veel hulga
maad suurendada.
Kui pargis olnuks
selliseid plaane neli, sel juhul oleks ka plaani peal selliseid plaane neli
ning iga pisikese plaani peal neli täppi tähistamas kaartide asukohti. Ja mitut
salvestatavat pilti näitavat ekraani filmides tunduks nagu eesolev koridor
muudkui hargneks ja hargneks ning kaugustesse kasvaval rägastikul ei paistagi
lõppu tulema.
Lõputu koridor
Mis on varem ekraanil,
maastikul või paberi peal olemas, seda saab ka ise luua ning oma soovi kohaselt
muuta. Kunstnikud ning teadlased on saanud niimoodi kauneid joone ja pinna
vahepealseid kujundeid - fraktaleid. Arvuti võimaldab meil aidata korduvaid
kujundeid uuesti ja uuesti välja joonistada ilma, et peaksime oma sõrmi tuhandete
väikeste joonekeste tõmbamiseks kulutama. Ning ega käsitsi korralikust
printerist selgemat tulemust ikkagi ei õnnestu saada. Ainult, et arvuti tarvis
tuleb jooned kõigepealt välja arvutada, alles siis võime hakata mõtlema nende
paberile kandmisele. Seetõttu tuleb hakkama saada mõnede matemaatiliste
arvutustega, kuid juhul kui need tunduvad ületamatutena, võib valemid võtta
juba töötavatest näidetest. Väärtusi suurendades ja vähendades ning käske
lisades ja eemaldades peaks olema võimalik pea igasugused vähegi
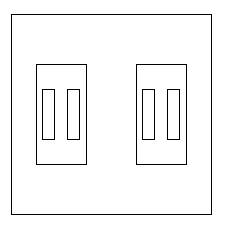
ettekujutatavad joonistused kokku kombineerida. Koridori moodustavate üksteise
sisse tulevate ringide või ristkülikute joonistamise eeskiri oleks küllalt
lihtne: tuleb neid senikaua üksteise otsa lükkida, kuni sisemised nii väikseks
muutuvad, et sinna sisse pole enam mõistlik ega võimalik midagi paigutada.
|
|
import java.awt.*; import java.applet.Applet; public class Koridor
extends Applet{ public
void paint(Graphics g){ int
x=100, y=100, laius=100, korgus=100;
while(laius>5){ g.drawRect(x, y, laius, korgus); laius=laius/2; korgus=korgus/2; x=x+laius/2; y=y+laius/2; } } } |
Niiviisi anti algul koridori ukse joonistamisel ette selle vasak ja ülemine
serv arvatuna pildi nullpunktist. Igal järgmisel korral joonistatakse ukse
sisse järgmine, mõõtmeid pidi poole väiksem uks (ehk praegusel juhul ristkülik.
Vasakut serva nihutakse edasi veerandi esialgse laiuse võrra. Nii paistab, et
järgmine jääb eelmise sisse keskele. Kui nihutaksime sisemist vähem, siis
tunduks, nagu seisaksime suure pika koridori suhtes viltu.
Iga sammuga ühekaupa
niimoodi kujundeid teise sisse või peale joonistada saab sellise tsükliga
ilusti. Lihtsalt tuleb iga ringi alguses ette anda uued koordinaadid, mille
järgi kujund välja joonistada. Iga sammuga mitme sisemise tüki joonistamine aga
läheb praegusel viisil keerukaks. Siit aitab meid välja rekursiooniks nimetatud
vahend, kus iseeneslikult kasvava kujundi loomine usaldatakse ühele
alamprogrammile, kust siis seda sama vajaduse korral uuesti välja kutsutakse.
Eelnev näide päistaks selle lähenemise valguses välja nii:
import java.applet.Applet;
import java.awt.*;
public class Koridor2 extends Applet{
void
joonistaKoridor(Graphics g, int x, int y, int laius, int korgus){
g.drawRect(x,
y, laius, korgus);
if(laius>5)joonistaKoridor(g, x+laius/4, y+korgus/4, laius/2,
korgus/2);
}
public
void paint(Graphics g){
joonistaKoridor(g, 100, 100, 100, 100);
}
}
Nagu näha, muutus kood pigem lühemaks ning mis tähtsam - kergemini
soovikohaselt muudetavaks. Loodud joonistamise käsku võib mitmelt poolt välja
kutsuda ning kui on soovi omale hargnevad koridorid luua, siis tuleb vaid paar
käsku ümber ja juurde teha.
import java.applet.Applet;
import java.awt.*;
public class Koridor3 extends Applet{
void
joonistaKoridor(Graphics g, int x, int y, int laius, int korgus){
g.drawRect(x, y, laius, korgus);
if(laius>15){
joonistaKoridor(g, x+laius/8,
y+korgus/4, laius/4, korgus/2);
joonistaKoridor(g, x+laius*5/8, y+korgus/4, laius/4, korgus/2);
}
}
public
void paint(Graphics g){
joonistaKoridor(g, 100, 100, 200, 200);
}
}
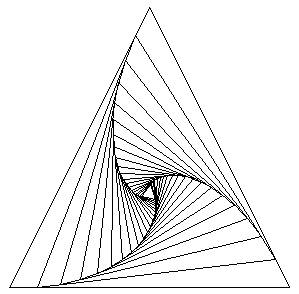
Teineteises peituvad hulknurgad
Kujundid ei pea üksteise sees mitte sama pidi olema. Küllalt lihne ning samas ilus on korduvalt veidi keeratuna hulknurki üksteise sisse joonistada. Hea ettekujutusvõime korral võib niimoodi jääda mulje kasvavast tornist või sügavusse pürgivast august. Kirjeldus:
Esimene kolmnurk joonistatakse nii, et tema kaugus rakendi servadest oleks 10 punkti. Järgmine kolmnurk joonistatakse eelmise sisse nõnda, et tema nurgapunktide leidmiseks liigutakse kümnendik mööda kolmnurga külge edasi. Matemaatiliselt leitakse uus asukoht võttes lähema punkti koordinaatidest üheksa kümnendikku ning liites sellele kaugema punkti ühe kümnendiku. Abimuutujatena kasutatakse siin jääki ja nihet, mis peavad oma väärtustes kokku andma ühe. Kõigepealt leitakse uued punktid ning seejärel omistatakse uute väärtused (ax1, ay1) joonistamisel kasutatavatele väärtustele(x1, y1). Sellline vaheetapp on vajalik, kuna algseid koordinaate läheb ka pärast uute leidmist vaja. Kõigepealt arvutatakse punkti 1 uus asukoht punktide 1 ning 2 vahelt. Kui aga pärast hakatakse kolmanda punkti uut asukohta arvutama punktide 1 ja 3 vahelt, siis peab punkti 1 vana asukoht teada olema, et leitud punkt algse joone peale satuks. Arvutatakse reaalarvudega, vaid joonistamisel teisendatakse täisarvulisteks ekraanipunktideks.
public class Kolmnurgad extends Applet{
public
void paint(Graphics g){
Dimension suurus=getSize();
double
x1=10, y1=suurus.height-10,
x2=suurus.width-10, y2=suurus.height-10,
x3=suurus.width/2, y3=10;
double
ax1, ay1, ax2, ay2, ax3, ay3;
int
kordustearv=20;
double
nihe=0.1, jaak=1-nihe; //osa külje pikkusest
for(int
i=0; i<kordustearv; i++){
g.drawLine((int)x1, (int)y1, (int)x2, (int)y2);
g.drawLine((int)x2, (int)y2, (int)x3, (int)y3);
g.drawLine((int)x3, (int)y3, (int)x1, (int)y1);
try{Thread.sleep(100);}catch(Exception e){} //viivitus
ax1=x1*jaak+x2*nihe;
ay1=y1*jaak+y2*nihe;
ax2=x2*jaak+x3*nihe;
ay2=y2*jaak+y3*nihe;
ax3=x3*jaak+x1*nihe;
ay3=y3*jaak+y1*nihe;
x1=ax1; y1=ay1;
x2=ax2; y2=ay2;
x3=ax3; y3=ay3;
}
}
}
Kolmnurgad üksteise seljas
Järgnevas näites asutakse
kolmnurka kasvatama. Võrdhaarsele kolmnurgale antakse ette pikema külje kaks
otspunkti. Nende abil arvutatakse kolmas nurk, mis paigutatakse pikema külje
keskkohast küljega risti võetuna poole küljepikkuse kaugusele. Külgede kohale
tõmmatakse jooned ning juhul, kui tekkinud lühem külg oli vähemalt 10 punkti
pikk, võetakse see uue kolmnurga pikimaks küljeks ning arvutatakse selle järgi
uued küljed. Kuna iga korraga lähevad tekkivad kolmnurgad väiksemaks, siis
ühest hetkest alates on mõistlik joonistamine ära lõpetada. Kui loodava
kolmnurga kõrguseks poleks mitte pool vaid kaks aluseks võetavat külge, siis
tuleksid uued kolmnurgad järjest suuremad ning tuleks teiselt poolt leida
ülempiir, millest suuremat kujundit pole enam mõistlik joonistada.
Joonistamise eest
hoolitseb meetod joonistaPuu, millele antakse joonistuse sihtkoha graafiline
kontekst ning joone otspunktide koordinaadid. Joonistamisega saab meetod
hakkama sõltumata sellest, millises asukohas ning millise kaldega joon sinna
ette antakse.
Matemaatilise poole
seletus. Eelkirjeldatud kohas asuva kolmanda punkti asukoha leidmiseks tuleks
kõigepealt leida pikema külje keskpunkt ning sealt edasi liikuda küljega risti
poole külje pikkuse ulatuses. Üks võimalus külje keskkoha leidmiseks on
arvutada nihe (vektor) ühest punktist teise (x=x2-x1; y=y2-y1), leida sellest
pool ning lisada esimese punkti koordinaatidele juurde (x=x1+(x2-x1)/2;
y=y1+(y2-y1)/2). Edasi tuleks leitud punktile otsa liita punktidevahelise
sirgega risti minev nihe. Nihkevektori keeramiseks saab kasutada seost
(x’=x*cos(a)-y*sin(a); y’=x*sin(a)+y*cos(a)) ehk täisnurkse vastupäeva nihke
korral cos(a)=0, sin(a)=1 ning (x’=-y;
y’=x) ning poole punktidevahelise kauguse pikkusega ning punktidevahelise
sirgega risti oleva nihke saab ((y2-y1)/2; (x2-x1)/2) ning sealtkaudu tulevad
kokku ka x3 ja y3 arvutamise valemid. Kuna arvutil on suunatud y-telg alla,
tavamatemaatikas aga üles, siis on märgid telje suuna muutmise eesmärgil
vastupidiseks muudetud.
Ootamiskäsk Thread.sleep
on vahele pandud lihtsalt seetõttu, et joonistamisel oleks näha, millises
järjekorras kolmnurgad ekraanile tekivad ning millal üks joonistuspuu valmis
saab ning teisega alustatakse. Kui see käsk välja kommenteerida, siis valmib
pilt tunduvalt kiiremini.
import java.applet.Applet;
import java.awt.*;
public class Puu extends Applet{
double
kaugus(int x1, int y1, int x2, int y2){
return
Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
}
void
joonistaPuu(Graphics g, int x1, int y1, int x2, int y2){
int x3=x1+(x2-x1)/2+(y2-y1)/2;
int y3=y1+(y2-y1)/2-(x2-x1)/2;
g.drawLine(x1, y1, x2, y2);
g.drawLine(x1, y1, x3, y3);
g.drawLine(x3, y3, x2, y2);
try{Thread.sleep(500);}catch(Exception e){}
if(kaugus(x1, y1, x3, y3)>10){
joonistaPuu(g, x1, y1, x3, y3);
joonistaPuu(g, x3, y3, x2, y2);
}
}
public
void paint(Graphics g){
joonistaPuu(g,
130, 290, 170, 290);
}
}
![]()
![]()
![]()
Kuna korduva joonistamise
puhul läheb punktidevaheliste nihkevektorite arvutamist ning keeramist sageli
vaja, siis koostati selle tarbeks klass, mis matemaatilised arvutused enese
sisse peidab ning programmeerijale jääb vaid hoolitseda sisulise poole eest.
Väärtused saab sellele klassile anda vaid isendi loomisel (samuti nagu klassi java.lang.String
puhul) ning iga muundamise puhul luuakse uus isend. Andmeid hoitakse ja
arvutatakse täpsuse huvides reaalarvudena, kuid välja antakse joonistamise
tarbeks täisarvudena. Meetodid on kahe nihke liitmiseks (pluss), teguriga korrutamiseks (korda), pikkuse
arvutamiseks (pikkus) ning täisnurga jagu vastupäeva keeramiseks (keera). Kuna
punkte tasandil võib andmete poolest samastada nullpunktist nendeni jõudvate
vektoritega, siis sobivad klassi meetodid mõnel puhul ka punktidega ümber
käimiseks.
public class Tasandinihe{
/**
* Nihke
koordinaatide väärtused. Piiritleja final rea ees näitab, et
*
väärtusi pärast algset omistamist enam muuta ei saa.
*/
final
double x, y;
public
Tasandinihe(double ux, double uy){
x=ux;
y=uy;
}
/**
* Nihe
arvutatakse etteantud kahe punkti koordinaatide järgi
*/
public
Tasandinihe(double x1, double y1, double x2, double y2){
x=x2-x1;
y=y2-y1;
}
int X(){
return
(int)x;
}
int Y(){
return
(int)y;
}
double
pikkus(){
return
Math.sqrt(x*x+y*y);
}
/**
* Vahe
samast punktist lähtuvate nihete otspunktide vahel.
*/
double
kaugus(Tasandinihe t1){
return
t1.miinus(this).pikkus();
}
/**
*
Väljastatakse nihke väärtuse ja teguri korrutis.
* Nihe
ise jääb muutmata.
*/
Tasandinihe korda(double tegur){
return
new Tasandinihe(x*tegur, y*tegur);
}
/**
*
Väljastatakse käesoleva ning parameetrina antud nihke summa.
* Mõlema
nihke enese väärtus jääb muutmata.
*/
Tasandinihe pluss(Tasandinihe t1){
return
new Tasandinihe(t1.x+x, t1.y+y);
}
Tasandinihe miinus(Tasandinihe t1){
return
this.pluss(t1.korda(-1));
}
/**
* Suund
keeratakse täisnurga jagu vastupäeva.
*/
Tasandinihe keera(){
return
new Tasandinihe(-y, x);
}
}
joonistamine näeks loodud Tasandinihkeklassi abil välja nii nagu allpool
toodud programmis Puu2. Leitakse kaks nihet: üks ühest punktist teise ning
teine nihe esimesega risti. Edaspidi saab neid kahte kasutada x ning y
ühikutena uues loodud koordinaatteljestikus, kus x-teljeks oleks kahe etteantud
punkti vaheline sirge.
Tasandinihe nx=p2.miinus(p1);
tähendab, et nihke x-ühiku leiame, kui lahutame teise punkti
koordinaatidest esimese punkti koordinaadid.
Eelmisega risti oleva y-ühiku saame aga x-i täisnurga jagu vastupäeva
keerates.
Tasandinihe ny=nx.keera();
Edasi võib loodud lõike ühikutena
kasutades leida joonistamise tarvis vajaliku(d) punkti(d). Niiviisi sõltubki
arvutatava joonise asukoht ja suurus vaid etteantud punktidest.
Tasandinihe p3=p1.pluss(nx.korda(0.5).pluss(ny.korda(-0.3)));
import java.applet.Applet;
import java.awt.*;
public class Puu2 extends Applet{
void
joonistaPuu(Graphics g, Tasandinihe p1, Tasandinihe p2){
Tasandinihe nx=p2.miinus(p1);
Tasandinihe ny=nx.keera();
Tasandinihe p3=p1.pluss(nx.korda(0.5).pluss(ny.korda(-0.3)));
g.drawLine(p1.X(), p1.Y(), p2.X(), p2.Y());
g.drawLine(p1.X(), p1.Y(), p3.X(), p3.Y());
g.drawLine(p3.X(), p3.Y(), p2.X(), p2.Y());
try{Thread.sleep(500);}catch(Exception e){}
if(p1.kaugus(p3)>10){
joonistaPuu(g, p1, p3);
joonistaPuu(g, p3, p2);
}
}
public
void paint(Graphics g){
joonistaPuu(g, new Tasandinihe(30, 290), new Tasandinihe(270, 290));
}
}
Et loodav joonis enam puu
moodi oleks, selleks peaks seal peale oksakohtade ka oksi endid olema. Nii
tuleb kaks punkti juurde arvutada ning iga kujund luuakse juba viie punkti
abil: algsed kaks oksa algul, järgmised kaks oksa lõpul ning veel üks, millest
alates uut oksapaari juurde arvutada. Joone tõmbamist läheb päris palju vaja,
selle tarvis sai uus alamprogramm loodud. Kui y suund kohe vastupidiseks
keerata, siis võib edaspidi harjumuspärast matemaatilist tava järgida, et see
telg ikka üles suunatud on. Muidugi veel viisakam oleks suunda alles
joonistamisel arvutada.
import java.applet.Applet;
import java.awt.*;
public class Puu3 extends Applet{
void
joonistaPuu(Graphics g, Tasandinihe p1, Tasandinihe p2){
Tasandinihe nx=p2.miinus(p1);
Tasandinihe ny=nx.keera().korda(-1); //y-suund vastupidiseks
Tasandinihe p3=p1.pluss(ny.korda(3));
Tasandinihe p4=p2.pluss(ny.korda(3));
Tasandinihe p5=p1.pluss(nx.korda(0.5).pluss(ny.korda(3.3)));
joon(g,
p1, p2);
joon(g,
p1, p3);
joon(g,
p2, p4);
joon(g,
p3, p5);
joon(g,
p4, p5);
try{Thread.sleep(500);}catch(Exception e){}
if(p1.kaugus(p3)>10){
joonistaPuu(g, p3, p5);
joonistaPuu(g, p5, p4);
}
}
void
joon(Graphics g, Tasandinihe t1, Tasandinihe t2){
g.drawLine(t1.X(), t1.Y(), t2.X(), t2.Y());
}
public
void paint(Graphics g){
joonistaPuu(g, new Tasandinihe(130, 290), new Tasandinihe(170, 290));
}
}
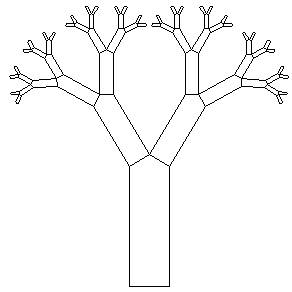
Kasutaja soovitud puu
Et kasutajale rohkem pildi kujundamise võimalusi anda, selleks võib algsed
punktid pärida tema käest, samuti lasta muuta muid parameetreid nagu okste
pikkus ja kalle ning joonistamise kiirus.
import java.applet.Applet;
import java.awt.*;
import java.awt.event.*;
public class Puu4 extends Applet implements
MouseListener{
int vajutusenr;
Tasandinihe hiir1=new Tasandinihe(130, 300),
hiir2=new Tasandinihe(170, 300);
Scrollbar
ooteaeg=new Scrollbar(Scrollbar.HORIZONTAL, 100, 100, 0, 500);
//väärtus, nupupikkus, vähim, suurim
Scrollbar
pikkus=new Scrollbar(Scrollbar.HORIZONTAL, 200, 100, 0, 500);
Scrollbar
kalle=new Scrollbar(Scrollbar.HORIZONTAL, 200, 100, 0, 500);
Label
ooteajasilt=new Label("Aeglustus joonistamisel:");
Label
pikkusesilt=new Label("Lüli pikkus:");
Label
kaldesilt=new Label("Okste kalle:");
public
Puu4(){
setLayout(new BorderLayout());
Panel
p1=new Panel(new GridLayout(3, 2));
p1.add(pikkusesilt);
p1.add(pikkus);
p1.add(kaldesilt);
p1.add(kalle);
p1.add(ooteajasilt);
p1.add(ooteaeg);
add(p1,
BorderLayout.SOUTH);
addMouseListener(this);
}
public
void mousePressed(MouseEvent e){
vajutusenr++;
if(vajutusenr==1){
hiir1=new Tasandinihe(e.getX(), e.getY());
}
if(vajutusenr==2){
hiir2=new Tasandinihe(e.getX(), e.getY());
repaint();
vajutusenr=0;
}
}
public
void mouseReleased(MouseEvent e){}
public
void mouseClicked(MouseEvent e){}
public
void mouseEntered(MouseEvent e){}
public
void mouseExited(MouseEvent e){}
void
joonistaPuu(Graphics g, Tasandinihe p1, Tasandinihe p2){
Tasandinihe nx=p2.miinus(p1);
Tasandinihe ny=nx.keera().korda(-1); //y-suund vastupidiseks
Tasandinihe p3=p1.pluss(ny.korda(pikkus.getValue()/100.0));
Tasandinihe p4=p2.pluss(ny.korda(pikkus.getValue()/100.0));
Tasandinihe p5=p1.pluss(nx.korda(0.5).pluss(ny.korda(
pikkus.getValue()/100.0+kalle.getValue()/1000.0
)));
joon(g,
p1, p2);
joon(g,
p1, p3);
joon(g,
p2, p4);
joon(g,
p3, p5);
joon(g,
p4, p5);
try{Thread.sleep(ooteaeg.getValue());}catch(Exception e){ }
if(p1.kaugus(p3)>10){
joonistaPuu(g, p3, p5);
joonistaPuu(g, p5, p4);
}
}
void
joon(Graphics g, Tasandinihe t1, Tasandinihe t2){
g.drawLine(t1.X(), t1.Y(), t2.X(), t2.Y());
}
public void
paint(Graphics g){
joonistaPuu(g, hiir1, hiir2);
}
public
static void main(String argumendid[]){
Frame
f=new Frame("Puu joonistamine");
f.add(new Puu4());
f.setSize(300, 400);
f.setVisible(true);
}
}
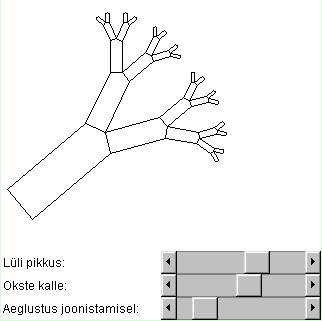
Joonistamisel ei pruugi
kõik lülid olla sugugi ühesugused. Nende ehitus võib sõltuda suurusest,
kaugusest juurest kui ka näiteks juhuse läbi. Nii võib luua küllalt usutavaid
pärisasjade analooge nagu lumehelves, riigipiir või kasvõi seesama puu. Ka
kõverjoone tõmbamise algoritmid kasutavad sarnast lähenemist, sest tunduvalt
odavam on meeles pidada kolme või nelja punkti asukohta kui joone iga punkti
asukohta. Liiatigi erinevad ekraanide ja printerite joonistustihedused
piisavalt, et ühe tarvis võib etteantud tihedusega punktide meeldejätmine
tunduda raiskamisena, teisel puhul aga jääb tulemus silmnähtavalt konarlik.
Rekursiivselt aga punkte ühendavaid sirgeid lühemateks lõikudeks jagades võib
igal korral uute joonte loomise siis lõpetada, kui ollakse jõutud
joonistustäpsuse tasemele. Sealt edasi arvutamine enam paremat tulemust ei saa
anda.
Ka võib kasutajal lubada
ette joonistada, milline peaks üks lüli välja nägema ning millistesse
kohtadesse selle peal võiksid uued kinnitada. Nii oleks tulemuseks töövahend
kunstniku tarvis. Kuid lihtsalt silmarõõmu võib sellistest joonistest küllaga
saada, pakkudes vaatajale järelemõtlemist, millal ja kus võib jälle midagi
kusagilt välja kasvama hakata.
Murdjoon
Üheks rekursiooni näiteks on murdjoone loomine. Olgu siis rakenduseesmärgiks lihtsalt kujundi servade kaunistamine või proovitagu läbi kapillaarsoonte võimalikku paiknemist nahaalusel pinnal. Kui pika joone sisse lisada jõnks ning edasi iga tekkinud joone sisse veel jõnks, siis ongi suudetud üheülbalise sirjoone asemel luua märgatavalt paindlikum kujund. Kavandatava algoritmina näeks joone jagamine väiksemateks osadeks välja järgnevalt.
public void
murdJoon(Graphics g, int x1, int y1, int x2, int y2){
if(kaugus(x1, y1, x2,
y2)>pikimaJoonePikkus){
//leiab joone keskkoha lähedale uue
punkti ning selle
//abil tõmbab kaks joont
} else {
g.drawLine(x1, y1, x2, y2);
}
}
Kuidas just uus punkt leitakse ning kuidas edasised jooned tehakse, selle tarvis on variante palju. Üks neist on toodud allpool. Joone keskoha võib leida otspunktide aritmeetilise keskmise abil.
int kx=(x1+x2)/2;
int ky=(y1+y2)/2;
Keskkoha lähedase punkti kaugus keskpunktist võiks sõltuda joone pikkusest. Et mida pikem joon, seda kaugemale võib nihke paigutada. Pika algse joone puhul pole väikest nihet kuigivõrd näha. Lühikese algjoone puhul aga sama pikk nihe võib loodavad jooned algsest hoopis pikemaks muuta ning juhul kui joone murdmine läheb kordusesse, võib kogu lugu sootuks tsüklisse sattuda. Katsete tulemusena aga paistis, et kui loodav punkt tuleb algsest keskkohast mõlemat telge pidi mõlemas suunas kuni 0,2 algse joone pikkuse kaugusele, siis pole joone liigset väljavenitatust karta. Samas aga on muutus piisav, et silmaga sirgjoont ja murdjoont eristada.
int x3=kx+(int)((Math.random()*k*0.4)-k*0.2);
int y3=ky+(int)((Math.random()*k*0.4)-k*0.2);
Kui uus keskpunkt valmis arvutatud, siis tuleb hoolitseda, et algsetest otspunktidest loodud uue punktini joon saaks loodud. Olgu siis lihtsalt tõmmatuna või võetakse nüüd ette sama algoritm mis ennegi ja püütakse uue joone liiga suure pikkuse korral see omakorda osadeks jagada.
murdJoon(g, x1, y1, x3, y3);
murdJoon(g, x3, y3, x2, y2);
Eelneva algoritmi põhjal veidi pikem koodinäide, mille käivitamisel peaks ka tulemus näha olema. Kui paint'is öeldakse
murdJoon(g, 10, 20, 150, 200);
siis asutakse etteantud punktide vahele joont tõmbama. Ning iga kord, kui loodud joon tuleb pikem kui määratud pikima joone pikkus ehk 20 jagatakse joon uuesti kaheks jupiks. Lühema kahe punkti vahelise kauguse puhul veetakse joon lihtsalt ekraanile ning edasi lühemaks ei jagata.
import
java.applet.Applet;
import
java.awt.*;
public
class Murdjoon2 extends Applet{
int pikimaJoonePikkus=20;
/**
* Alamprogramm väljastab kahe punkti
vahelise kauguse
*/
public double kaugus(int x1, int y1, int x2,
int y2){
int dx=x2-x1;
int dy=y2-y1;
return Math.sqrt(dx*dx+dy*dy);
}
public void murdJoon(Graphics g, int x1, int
y1, int x2, int y2){
double k=kaugus(x1, y1, x2, y2);
if(k>pikimaJoonePikkus){
int kx=(x1+x2)/2;
int ky=(y1+y2)/2;
int
x3=kx+(int)((Math.random()*k*0.4)-k*0.2);
int
y3=ky+(int)((Math.random()*k*0.4)-k*0.2);
murdJoon(g, x1, y1, x3, y3);
murdJoon(g, x3, y3, x2, y2);
} else {
g.drawLine(x1, y1, x2, y2);
}
}
public void paint(Graphics g){
murdJoon(g, 10, 20, 150, 200);
}
public static void main(String[]
argumendid){
Frame f=new Frame();
f.add(new Murdjoon2());
f.setSize(300, 300);
f.setVisible(true);
}
}

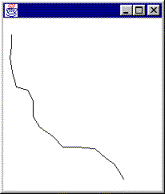

Igal joonistusel uus murdjoon
Eelnenud näites tuli igal joonistuskorral asuda joont uuesti välja arvutama. Tahtes aga masinat liigsest nuputamisest säästa ning mis tähtsamgi - loodud joont ikka ja jälle uuesti vaadata, tuleb mõeldud punktid meelde jätta. Et loodavate punktide hulk pole ette teada, siis on nende hoidmiseks massiivi asemel mugavam kasutada nimistut, näiteks standardpaketis kättesaadavat LinkedListi. Ning kuna siinses näites joone lühim pikkus ei muutu, siis võib kõik vahepunktid algul välja arvutada ning edasi vaid sobival hetkel pilt mälus paiknevate andmete põhjal välja joonistada. Punkti andmete hoidmiseks võib kasutada java.awt paketis asuvat klassi Point - vahendit mis juba olemas, ei pea hakkama enam uuesti looma. Ka punktide vahelise kauguse leidmiseks on juba käsklus olemas, Point-isendi käsklus distance teatab sobiva väärtuse. Tsükliga küsitakse nimistust ükshaaval välja punktipaarid. Kui punktide vaheline kaugus ületab lubatud pikima, siis leitakse keskkoha lähedale uue punkti koordinaadid nii nagu eelmiseski näites. Loodud p3 asetatakse endise p2 kohale ning LinkedList hoolitseb juba ise, et ülejäänud elemendid nimistus edasi liigutataks. Joonistamisel piisab punktipaaride näidatavate ekraanikoordinaatide vahele jooned tõmmata ning murdjoon ongi ekraanil.
import
java.applet.Applet;
import
java.awt.*;
import
java.util.*;
public
class Murdjoon4 extends Applet{
LinkedList punktid=new LinkedList();
int pikimaJoonePikkus=5;
public Murdjoon4(){
punktid.add(new Point(10, 10));
punktid.add(new Point(200, 300));
lisaVahePunktid();
}
public void lisaVahePunktid(){
int koht=0;
while(koht+1<punktid.size()){
Point p1=(Point)punktid.get(koht);
Point p2=(Point)punktid.get(koht+1);
double kaugus=p1.distance(p2);
if(kaugus>pikimaJoonePikkus){
Point p3=new Point(
(p1.x+p2.x)/2+(int)((Math.random()-0.5)*0.4*kaugus),
(p1.y+p2.y)/2+(int)((Math.random()-0.5)*0.4*kaugus)
);
punktid.add(punktid.indexOf(p2), p3);
if(p1.distance(p3)<=pikimaJoonePikkus){
koht=koht+1;
}
} else {
koht=koht+1;
}
}
}
public void paint(Graphics g){
for(int i=0; i<punktid.size()-1; i++){
Point p1=(Point)punktid.get(i);
Point p2=(Point)punktid.get(i+1);
g.drawLine(p1.x, p1.y, p2.x, p2.y);
}
}
public static void main(String[]
argumendid){
Frame f=new Frame();
f.add(new Murdjoon4());
f.setSize(300, 300);
f.setVisible(true);
}
}


Joon püsib ka akna suuruse muutmisel
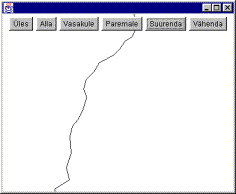
Virtuaalne Eestimaa
Järgnevalt näide, mille alusel peaks õnnestuma ehitada isearenevaid maailmu nii mängude kui õpisimulatsioonide tarbeks. Nii nagu astronoomid väidavad, et mida pole võimalik märgata, seda ei pruugi ka olemas olla, kehtib sarnane järeldus seda enam ka arvutimaailma kohta. Sugugi ei pruugi kõiki erijuhte kohe programmi töö algul välja mõelda. Kui täpsustused suudetakse vajalikul hetkel tehe piisavalt kärmesti, pole kasutajal kuigivõrd võimalusi otsustamiseks, et mudelil kaugvaate korral miskit viga oleks. Ning võimalus igas soovitud detailis pisiasjadeni välja minna jätab vaatajale uskumuse, et kõik ongi lõpuni viimistletud. Kui kontrollid tulevad majapidamist üle vaatama ning kõikjal kuhu vaadata valitseb kord ja puhtus, ei saa neil jorisemiseks põhjust olla. Olgugi, et võibolla lihtsalt keegi jälgib kontrollide teekonda ning hoolitseb, et iga võimalik vaadeldav punkt õnnestuks selleks ajaks korda teha, kui kontroll oma suurima kiiruse abil saaks sinna jõuda.
Või kõrvutuseks veel näide muinasjutuvestjast. Hea vestja suudab väljamõeldud maailma kõikide kohtade ja erijuhtude kohta vastuseid anda, ehkki ta ei pruugi olla algul kõike lõpuni välja mõelnud. Kui ta suudab hoolitseda, et loodavad paigad, ühendusteed ja sündmused eelnevatega vastuollu ei lähe, siis võib jutustaja kasvõi koos kuulajatega uusi lugusid ja kohti välja mõelda. Ikka on huvitav kuulata, kaasa mõelda ja meenutada.
Võrreldes eelmise näitega ei saa praegusel juhul kõiki punkte rakenduse töö algul välja mõelda, vaid tuleb kohti vastavalt kasutaja liikumisele juurde mõelda. Kui kilomeetritepikkune murdjoon kohe sentimeetripikkuste lõikude kaupa välja arvutada, siis kuluks mälu kõvasti ning joonistamine muutub lootusetult aeglaseks. Juba ainuüksi ühe kilomeetri peale tuleks sada tuhat punkti, pikema maa peale seda enam.
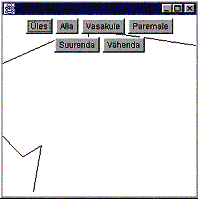
Väljamõeldud võlumaailma aluseks on Eestimaa väga ligikaudne rannajoon - nii umbes Euroopa ilmakaardilt vaadatuna. Ning kes siinsest kandist rohkem ei tea, võib nähtud pilti täiesti uskuma jääda - eriti kuna uuesti samasse kohta vaatama tulles rannajoon viimati vaadatuga võrreldes ikka samal kohal paikneb.
Kasutajaliidesesse tulid juurde nupud, et oleks võimalik nii igasse ilmakaarde kui üles ja allapoole liikuda. Horisontaalsuunas on arvestatud, et üks ühik võrdub ligikaudu ühe kilomeetriga. Kõrguse puhul aga lihtsalt muudetakse suurendust iga sammu juures sama koefitsiendi jagu. Punkti andmete hoidmiseks kasutatakse endise täisarvulise Point'i asemel Point2D.Double-t mis võimaldab asukohti tunduvalt täpsemalt meelde jätta. Täisarvude puhul oleks siinse mõõtkava juures ühele punktile vastav üks kilomeeter, mis aga oleks külade ja linnade loomise soovi korral ilmselt liiga suur mõõtühik.
Maailmakoordinaatidest ekraanikoordinaatide arvutamiseks loodi eraldi funktsioon nagu ikka selliste arvutuste puhul tavaks. Punkti ekraanile joonistamisel arvestatakse nii punkti enese maailmakoordinaate, vaataja asukohta, suurendust kui akna suurust ja sealt tulenevat ekraani keskkoha koordinaadi väärtust. Koht, mis paikneb vaatamisel akna keskel, jääb sinna ka suurendamise või vähendamise korral.
int ekraaniX(double maailmaX){
return
ekeskx+(int)((maailmaX-vx)*suurendus);
}
Edasi kommenteeritud rakenduse kood.
import
java.applet.Applet;
import
java.awt.*;
import
java.awt.geom.*;
import
java.util.*;
import
java.awt.event.*;
public
class Murdjoon6 extends Applet implements ActionListener{
/** Ülesliikumisnupp. Vaataja koordinaadid
vähenevad */
Button yles=new Button("Üles");
/** Allaliikumisnupp. Vaataja liigub lõuna
suunas */
Button alla=new Button("Alla");
/** Nupp läände liikumiseks */
Button vasakule=new
Button("Vasakule");
/** Nupp itta liikumiseks */
Button paremale=new
Button("Paremale");
/**
* Pilt suureneb liigutakse allapoole.
* Nähtava osa joonele arvutatakse vajadusel
punkte juurde.
*/
Button suurenda=new
Button("Suurenda");
/**
* Suurenduskordaja väheneb. Näiliselt
liigutakse maapinnast kaugemale.
*/
Button vahenda=new
Button("Vähenda");
/**
* Kindlaksmääratud rannajoone punktide
loetelu maailmakoordinaatides.
*/
LinkedList punktid=new LinkedList();
/**
* Nähtav pikkus ekraanipunktides, millest
alates asutakse joont poolitama.
*/
double pikimJoonEkraanil=30;
/**
* Vaataja asukoha x maailmakoordinaatides.
*/
double vx=286;
/**
* Vaataja asukoha y maailmakoordinaatides.
*/
double vy=120;
/**
* Vaataja algne samm maailmakoordinaatides.
*/
double vsamm=5;
/**
* Ekraani keskkkoha x.
*/
int ekeskx;
/**
* Ekraani keskkkoha y.
*/
int ekesky;
/**
* Koefitsient näitamaks, mitu ekraanipunkti
vastab ühele
* maailmakoordinaatides ühikule.
*/
double suurendus=1;
/**
* Suhe, mille jagu suurenduskoefitsient
suureneb või väheneb
* alla või üles liikumisel.
*/
double suurenduskordaja=1.1;
/**
* Kujunduse, kuularite ja algväärtuste
paikasättimine.
*/
public Murdjoon6(){
add(yles);
add(alla);
add(vasakule);
add(paremale);
add(suurenda);
add(vahenda);
yles.addActionListener(this);
alla.addActionListener(this);
vasakule.addActionListener(this);
paremale.addActionListener(this);
suurenda.addActionListener(this);
vahenda.addActionListener(this);
looAlgneJoon();
}
/**
* Algse rannajoone punktide sättimine
maailmakoordinaatides.
*/
void looAlgneJoon(){
punktid.add(new Point2D.Double(186, 249));
punktid.add(new Point2D.Double(198, 180));
punktid.add(new Point2D.Double(170, 197));
punktid.add(new Point2D.Double(129, 155));
punktid.add(new Point2D.Double(129, 61));
punktid.add(new Point2D.Double(219, 21));
punktid.add(new Point2D.Double(267, 27));
punktid.add(new Point2D.Double(270, 6));
punktid.add(new Point2D.Double(352, 17));
punktid.add(new Point2D.Double(455, 33));
}
/**
* Liigutamine vastavalt nupuvajutustele.
*/
public void actionPerformed(ActionEvent e){
double samm=vsamm/suurendus;
if(e.getSource()==yles) {vy-=samm;}
if(e.getSource()==alla) {vy+=samm;}
if(e.getSource()==vasakule){vx-=samm;}
if(e.getSource()==paremale){vx+=samm;}
if(e.getSource()==suurenda){
suurendus*=suurenduskordaja;
}
if(e.getSource()==vahenda){suurendus/=suurenduskordaja;}
repaint();
}
/**
* Lisatavate punktide arvutus. Kui kahe
punkti vaheline joon ekraanil
* kipub tulema suurem määratud väärtusest,
siis leitakse
* joone keskkoha lähedale uus punkt ning
tõmmatakse algse joone
* otspunktidest jooned sellesse punkti.
*/
public void lisaVahePunktid(){
double
pikimaJoonePikkus=pikimJoonEkraanil/suurendus;
int koht=0;
while(koht+1<punktid.size()){
Point2D.Double
p1=(Point2D.Double)punktid.get(koht);
Point2D.Double
p2=(Point2D.Double)punktid.get(koht+1);
double kaugus=p1.distance(p2);
if(kaugus>pikimaJoonePikkus &&
(kasSees(p1.x, p1.y) || kasSees(p2.x, p2.y))){
Point2D.Double p3=new Point2D.Double(
(p1.x+p2.x)/2+((Math.random()-0.5)*0.4*kaugus),
(p1.y+p2.y)/2+((Math.random()-0.5)*0.4*kaugus)
);
punktid.add(punktid.indexOf(p2), p3);
if(p1.distance(p3)<=pikimaJoonePikkus){
koht=koht+1;
}
} else {
koht=koht+1;
}
}
}
/**
* Maailmakoordinaatide teisendus
ekraanikoordinaatideks, arvestatakse
* suurendust ja kasutaja asukohta.
*/
int ekraaniX(double maailmaX){
return
ekeskx+(int)((maailmaX-vx)*suurendus);
}
/**
* Maailmakoordinaatide teisendus ekraanikoordinaatideks.
*/
int ekraaniY(double maailmaY){
return
ekesky+(int)((maailmaY-vy)*suurendus);
}
/**
* Kontroll, kas etteantud
maailmakoordinaatidega punkt mahub
* ekraanil vaatevälja.
*/
boolean kasSees(double maailmaX, double maailmaY){
int ex=ekraaniX(maailmaX);
int ey=ekraaniY(maailmaY);
return ex>0 &&
ex<getWidth() && ey>0 && ey<getWidth();
}
/**
* Mälus olevatele andmetele vastavalt
koostatakse ekraanile pilt.
* Nähtava ala piires palutakse punkte luua niivõrd,
et pikim
* näha olev joon ei ületaks määratud
pikkust.
*/
public void paint(Graphics g){
lisaVahePunktid();
ekeskx=getWidth()/2;
ekesky=getHeight()/2;
for(int i=0; i<punktid.size()-1; i++){
Point2D.Double p1=(Point2D.Double)punktid.get(i);
Point2D.Double
p2=(Point2D.Double)punktid.get(i+1);
g.drawLine(ekraaniX(p1.getX()),
ekraaniY(p1.getY()),
ekraaniX(p2.getX()),
ekraaniY(p2.getY()));
}
}
/**
* Käivitus käsurealt.
*/
public static void main(String[]
argumendid){
Frame f=new Frame();
f.add(new Murdjoon6());
f.setSize(300, 300);
f.setVisible(true);
}
}
|
Algne üksikute punktidega rannajoon |
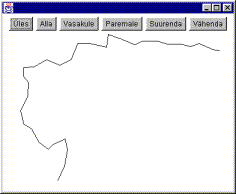
Rannajoon pärast esimest punktide lisamist |
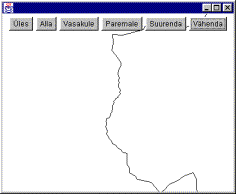
|
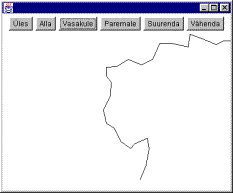
Lääneranniku nihutus pildi keskele |
Suurendus koos üksikute lisandumistega |
|
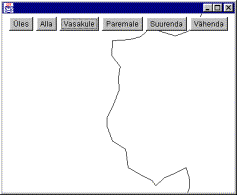
Lähivaade |
Algsest säbrulisema üldplaan vaatepaigas. |
Et illustreerimise mõttes oli pikima joone pikkuseks määratud 30 ekraanipunkti, siis paistab algne suurte nurkadega joon selgelt välja. Kui suurimaks lubatud pikkuseks panna aga näiteks kaks punkti, siis pole kasutajal kuigivõrd võimalust märgata, et algne nähtav kaart polegi kõikide võimalike hiljem vaadatavate kohtade pealt veel olemas. Et vaatama asumisel vastavad kohad kohe luuakse, võiks mulje jäädagi täiuslik.
Fraktali omaduste demonstreerimisel võibki lubada üha peenemaks minevat arvutust. Mingil hetkel kipub niimoodi Double 14st komakohast täpsusel väheks jääma ning tuleks leida miski täpsem võimalus koordinaatide arvutamiseks. Olgu selleks siis java.math.BigDecimal soovitud arvu komakohtade talletamiseks või mõni omaloodud vastava oskusega objekt. Kusjuures suuremat komakohtade arvu on vaja talletada vaid lähemal vaatlusel tekkivate punktide korral.
Kui eesmärgiks aga tegeliku keskkonna piisavalt tõetruu jäljendamine, siis võiks koos suurendusega muutuda ka tekkivate kujundite omadused. Kui simuleeritakse õhusõidukiga Eestimaa kohal lendamist, siis tõenäoliselt pole põhjust välja arvutada vähem kui sentimeetrise läbimõõduga objekte. Samas ei pruugi nähtav ja täienev osa piidruda sugugi vaid rannajoonega.
Ülesandeid
Virtuaalse
Eestimaa täiendus
· Täienda rannajoont, lisa Eestimaale ka ida- ja lõunapiir.
· Nähtavad jooned võivad jaguneda mitmesse kogumisse. Lisa eraldi kogumina Võrtsjärve rannajoon.
· Iga kogumi juures on lisaks punktile kirjas ka vastava joone värv.
· Sinise värviga tähista tähtsamad jõed. Ka neile mõeldakse lähemal vaatamisel välja käänakud.
· Jõgede ja rannajoone käänakute juures ei lähe joone pikkus väiksemaks kui 1 meeter.
· Alates suurendusest 1 ekraanipunkt = 10 meetrit hakatakse välja mõtlema ning näitama puid. Kord loodud puud jäävad samadele kohtadele.
Naerunägu
· Joonista naeratav nägu, kelle kummaski silmas oleks samuti naerunägu.
· Joonise suurendamisel ilmub igast silmast jälle uus naerunägu välja.
· Lisaks eelmisele saab kasutaja panna joonise pidevalt suurenema ning määrata näo kallet.
Viisnurgad
· Ekraanile joonistatakse viisnurk.
· Üha väiksemad erivärvilised seest täidetud viisnurgad on üksteise sees, kusjuures sisemise viisnurga tipp läheb välimise viisnurga serva keskkohta.
· Üksteise sees on kuni 100 viisnurka. Kerimisribaga saab määrata, millise koha peal sisemise viisnurga nurk välimise serva puutub.