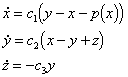
The dynamical system
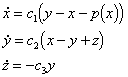
where
![]()
represents a mathematical model of
an LRC circuit consisting of a linear resistance, two linear capacitances,
a linear inductance and a non-linear diode. The parameters of the system
satisfy ![]() ,
, ![]() .
.
There are three equilibrium points
![]()
The characteristic polynomial for the equilibrium point at the origin is
![]()
Thus ![]() and
hence the equilibrium point is unstable.
and
hence the equilibrium point is unstable.
The characeristic polynomials for the two equilibria are identical and given by
![]()
There is a bifurcation at
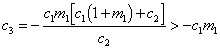
where the equilibrium point changes
from unstable to stable as ![]() becomes
greater than the bifurcation value.
becomes
greater than the bifurcation value.
SIMULATION
Taking parameter values ![]() the
critical value of
the
critical value of ![]() .
The plots below show the behaviour of the system as
.
The plots below show the behaviour of the system as ![]() is
decreased.
is
decreased.
![]()
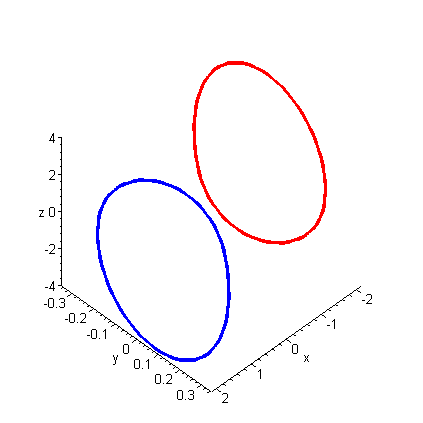
Pair of Limit Cycles
![]()
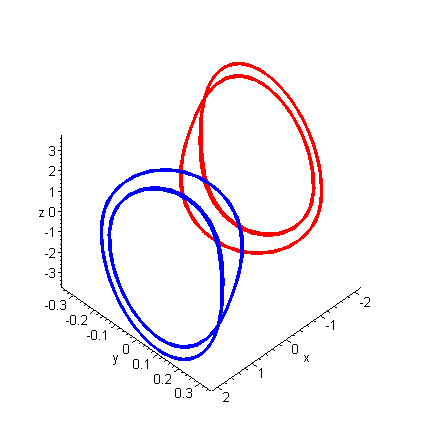
Period Doubling
![]()
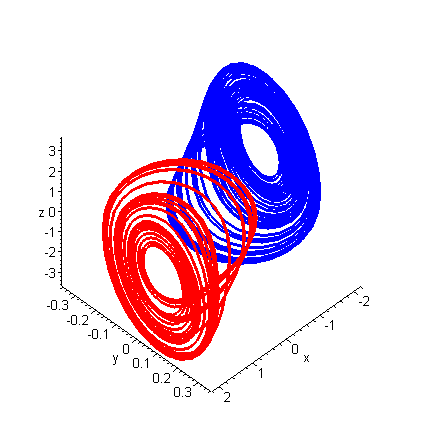
Two Strange Attractors
![]()
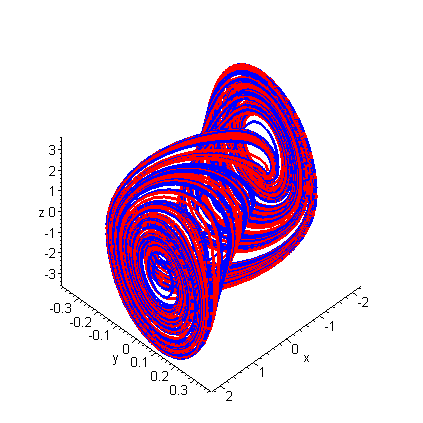
The Double Scroll Attractor
The link below provides a Java simulation of the system.
Parameter values and initial conditions can be changed.
An alternative series of simulations is available using Maple.