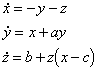
The dynamical system
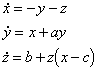
was constructed by the Swiss mathematician Otto
Rössler as the minimum system required to exhibit chaos. Note
that the autonomous system only has one nonlinear term, 
in the third equation. Despite its simplicity this system is much harder
to analyse than the Lorenz system.
There are two equilibrium points of the system given by
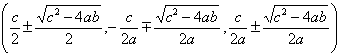
These equilibria only exist provided that 
.
The first equilibrium point (taking the plus sign) is unstable. The stability of the second equilibrium point depends on the parameter values and can be stable or unstable.
PHASE SPACE
We shall fix the parameters 
and
explore the behaviour of the system as c is increased from 2.5 to
5.
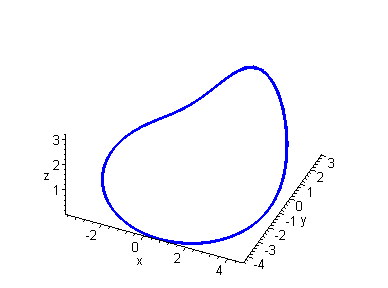
Limit Cycle
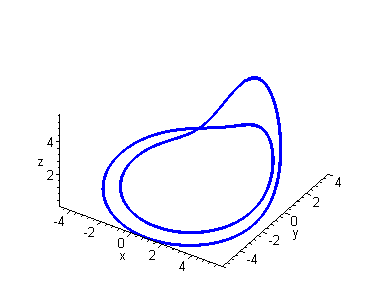
Period Doubling
The attractor has undergone a period doubling in which the attractor
consists of two loops which are both traversed before the motion is repeated.
This behaviour can be clearly seen from the time series plot.
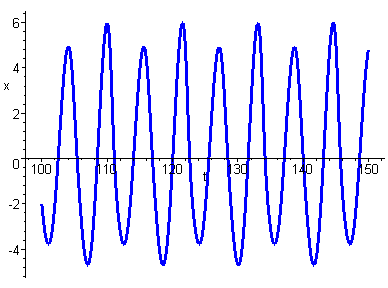
Notice that there are two distinct sets of peaks and troughs and the period of the motion is approximately twice that of the limit cycle.
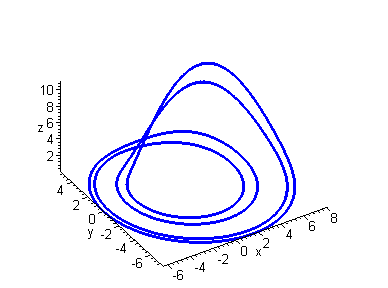
Further Period Doubling
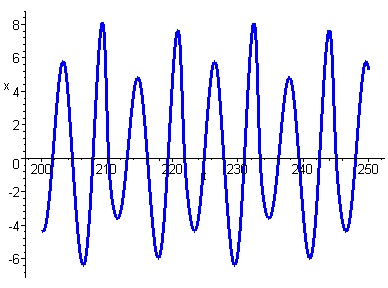
Now we have a further period doubling with four distinct sets of peaks and troughs.
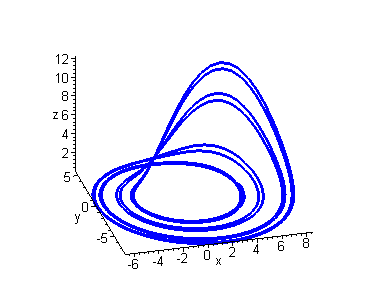
Further Period Doubling
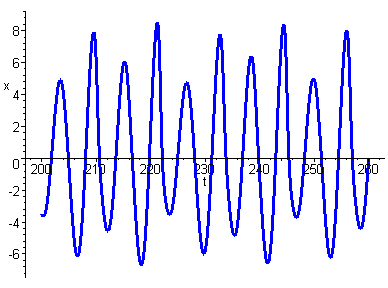
Now we have eight distinct sets of peaks and troughs and a further period doubling. This period doubling continues as we increase c. However a point is reached at which period doubling ceases and we obtain a strange attractor. This could be thought of a periodic attractor with infinite period.
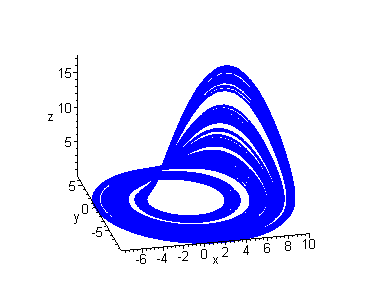
Strange Attractor
The behaviour of the Rössler system illustrated above is characteristic of many dynamical systems which exhibit chaos. The behaviour is often referred to as a period doubling cascade.