Thus far we have examined the occurence of chaos in autonomous systems of differential equations of dimension greater than two. Although the Poincaré-Bendixson Theorem guarantees that chaos cannot occur in autonomous systems of dimension two this is not necessarily true for non-autonomous systems. To investigate the occurence of chaos in such systems consider the equation below
This equation can be rewritten as an autonomous first order system by
using the transformations 
resulting in the autonomous system of three equations
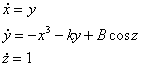
Notice that the system contains all the features necessary for the occurrence
of chaotic behaviour i.e. it is a nonlinear autonomous system in three
dimensions. The system has no equilibria in three dimensions since 
is never equal to zero. In plotting the trajectories of the system it is
only necessary to consider the projection onto the x-y plane since
the variable z has only been introduced as a device to make the system
autonomous. Note that the resulting plot is not a true phase portrait of
the system.
The system exhibits extremely complex behaviour and some features will
be investigated in the exercises. Here we consider the behaviour of the
system for 
and increasing values of B.
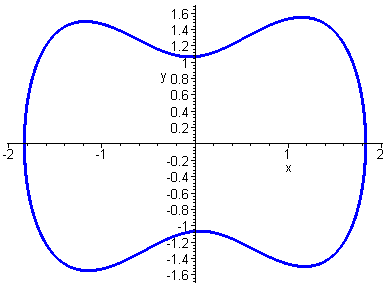
Limit Cycle
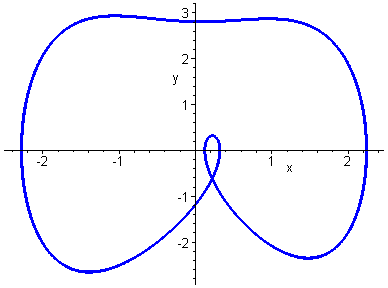
Periodic Attractor
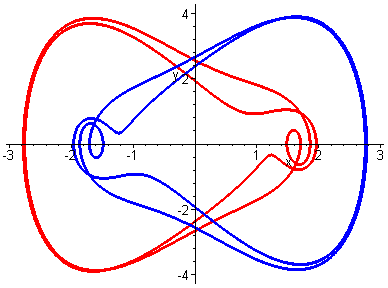
Two Periodic Attractors
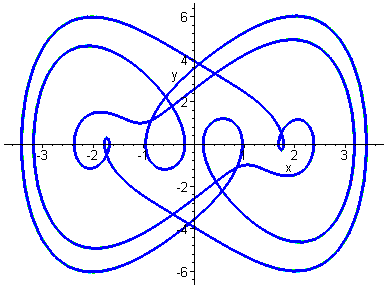
Single Periodic Attractor
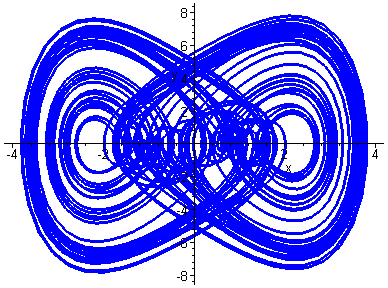
Strange Attractor