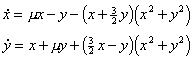
The behaviour of a one-dimensional dynamical system may depend on the value of a certain parameter. As the parameter value passes through a critical value the system dynamics can change substantially. This is termed a bifurcation. Consider the following example.
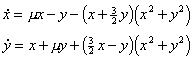
It can be shown that the polar form of the system is
![]()
from which it is clear that there is a single equilibrium point at the origin. The first polar equation can be written as
![]()
Clearly there is a limit cycle of radius ![]() in
this case. Also the origin is unstable since for small r
in
this case. Also the origin is unstable since for small r
![]()
which is positive.
If ![]() then
then ![]() and
the origin is globally asymptotically stable. This behaviour is illustrated
below for the cases
and
the origin is globally asymptotically stable. This behaviour is illustrated
below for the cases ![]() and
and ![]() respectively.
respectively.
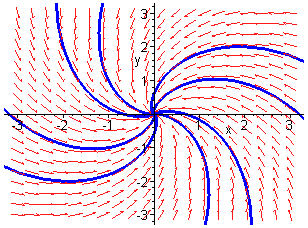
Stable Focus
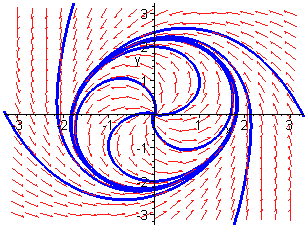
Unstable Focus + Stable Limit Cycle
We see that as the parameter ![]() passes
through zero from negative to positive a stable focus gives way to an unstable
focus surrounded by a stable limit cycle whose radius increases with
passes
through zero from negative to positive a stable focus gives way to an unstable
focus surrounded by a stable limit cycle whose radius increases with ![]() .
This is an example of a Hopf bifurcation.
.
This is an example of a Hopf bifurcation.
In order to gain further insight into the behaviour of this system and to set the scene for the introduction of the principal result of this section let us carry out a linear stability analysis of the cartesian form of the equations. The linearization about the origin is obviously
![]()
The Jacobian matrix is therefore
![]()
The eigenvalues are given by
![]()
Solving gives
![]()
Thus if ![]() we
have a stable focus, if
we
have a stable focus, if ![]() an
unstable focus and if
an
unstable focus and if ![]() we
cannot decide (although we know from the polar form that we have a stable
focus). As the bifurcation from a stable focus to an unstable focus surrounded
by a stable limit cycle occurs the real part of the eigenvalues changes
from negative to positive being zero at the bifurcation point. This is
typical of this type of Hopf bifurcation which is said to be supercritical.
The following theorem generalises these results.
we
cannot decide (although we know from the polar form that we have a stable
focus). As the bifurcation from a stable focus to an unstable focus surrounded
by a stable limit cycle occurs the real part of the eigenvalues changes
from negative to positive being zero at the bifurcation point. This is
typical of this type of Hopf bifurcation which is said to be supercritical.
The following theorem generalises these results.
Theorem - The Hopf Bifurcation Theorem
Suppose that the system
![]()
has an equilibrium point at the origin for all ![]() .
In addition suppose that the eigenvalues
.
In addition suppose that the eigenvalues ![]() of
the linearization are purely imaginary when
of
the linearization are purely imaginary when ![]() .
If the real part of the eigenvalues satisfy
.
If the real part of the eigenvalues satisfy
![]()
and the origin is asymptotically stable when ![]() then
then
In the previous example(i)is a bifurcation point of the system;
(ii) for some
such that
the origin is a stable focus;
(iii) for some
such that
the origin is an unstable focus surrounded by a stable limit cycle whose size increases with
.
![]()
and hence the theorem predicts the existence of the stable limit cycle.
![]()
as the parameter![]() is
varied.
is
varied.
This system has a single equilibrium point at the origin as you should verify. The linearization is clearly
![]()
which is identical to that found in Worked Example 6. This means that
all the conditions of the Hopf bifurcation theorem are satisfied apart
from the asymptotic stability of the origin at ![]() .
This suggests that there may be a Hopf bifurcation. However the polar form
of the equation for r is
.
This suggests that there may be a Hopf bifurcation. However the polar form
of the equation for r is
![]()
which shows that the origin is unstable. Hence the theorem does not
apply. Using Maple we obtain the following plots for ![]() and
and ![]() respectively.
respectively.
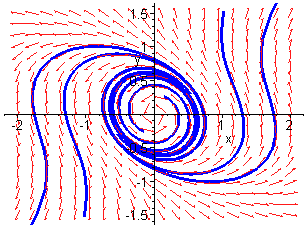
Stable Focus + Unstable Limit Cycle
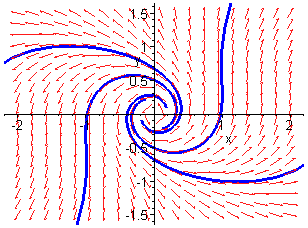
Unstable Focus
The first plot shows the existence of an unstabe limit cycle surrounding
the stable focus at the origin The second plot shows the unstable focus
which occurs when ![]() is
positive. We have a different type of Hopf bifurcation which is referred
to as subcritical.
is
positive. We have a different type of Hopf bifurcation which is referred
to as subcritical.
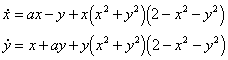
undergoes a subcritical Hopf bifurcation at ![]() for
a certain range of values of the parameter a.
for
a certain range of values of the parameter a.
Clearly an E.P. at the origin.
Transforming to polar coordinates
![]()
Thus for ‘small’ values of r
![]()
and hence the equilibrium point is a stable focus if ![]() and
an unstable focus if
and
an unstable focus if ![]() .
.
For ![]()
![]()
for ‘small’ r. Thus the origin is unstable.
Now we can factorise the expression for ![]() to
obtain
to
obtain
![]()
If ![]() then
then ![]() are
both real and positive so we can further factorise to obtain
are
both real and positive so we can further factorise to obtain
![]()
and thus we obtain two limit cycles of radii ![]() and
and ![]() .
Examining the signs of the terms in the factorisation
.
Examining the signs of the terms in the factorisation
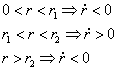
Thus ![]() is
unstable and
is
unstable and ![]() is
stable.
is
stable.
If ![]() then
then ![]() is
real and positive but
is
real and positive but ![]() is
real and negative. In this case we can only factorise into the form
is
real and negative. In this case we can only factorise into the form
![]()
and thus there is a single limit cycle of radius ![]() .
Examining the signs of the terms in the factorisation
.
Examining the signs of the terms in the factorisation
![]()
and thus the limit cycle is stable.
Summarising these results we see that if ![]() the
origin is a stable focus surrounded by an unstable limit cycle of radius
the
origin is a stable focus surrounded by an unstable limit cycle of radius ![]() and
a stable limit cycle of radius
and
a stable limit cycle of radius ![]() .
If
.
If ![]() the
origin is an unstable focus surrounded by a stable limit cycle of radius
the
origin is an unstable focus surrounded by a stable limit cycle of radius ![]() .
.
Thus there is a subcritical Hopf bifurcation. The existence of the second stable limit cycle does not affect this conclusion.