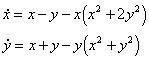
It is not always possible to determine the existence of a limit cycle directly from the polar form as is illustrated in the following example.
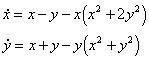
has a stable limit cycle which lies in the annular region
![]()
The polar form of the system is
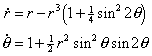
Note that the polar form does not immediately give a limit cycle.
If ![]()
![]()
But this must be true for all ![]() .
This
means that
.
This
means that
![]()
If ![]()
![]()
But this must be true for all ![]() .
This
means that
.
This
means that
![]()
These results imply that ![]() when
when ![]() and
and ![]() when
when ![]() .
.
Consider a trajectory which starts inside the annular region ![]() shown
below.
shown
below.
![]()
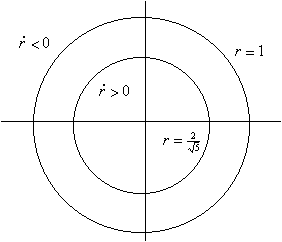
Suppose that the trajectory touches the outer boundary. Then immediately ![]() and
the trajectory is forced to remain in the annulus. Similarly if the trajectory
touches the inner boundary then
and
the trajectory is forced to remain in the annulus. Similarly if the trajectory
touches the inner boundary then ![]() and
once more the trajectory is forced to remain in the annulus. Thus any trajectory
which starts inside the annulus is trapped within it. Such a region is
called a trapping region.
and
once more the trajectory is forced to remain in the annulus. Thus any trajectory
which starts inside the annulus is trapped within it. Such a region is
called a trapping region.
There are no equilibrium points within the annulus. Intuitively since a trajectory cannot tend to an equilibrium point and cannot cross itself the trajectory must either be a closed orbit or eventually tend to a closed orbit. Hence there must be at least one limit cycle within the annulus.