.
However in practice we must deal with finite stepsizes. To illustrate the
problems that might arise consider the mid-point method
So far we have considered the behaviour of numerical methods in the
limit as the stepsize .
However in practice we must deal with finite stepsizes. To illustrate the
problems that might arise consider the mid-point method
This is a linear two-step method. In standard form the method is
thus
Checking consistency
The roots of 
are given by 
hence the method is both consistent and zero-stable and hence convergent.
Now consider the solution of the initial value problem
by the mid-point method using a stepsize 
.
Using Maple we obtain the plot
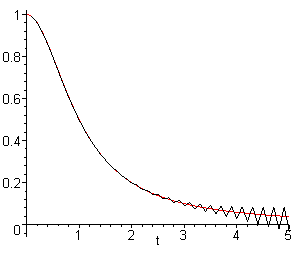
Notice that the numerical solution becomes increasingly innacurate,
oscillating about the exact solution, as t increases. This behaviour
arises because the behaviour of the numerical solution does not mimic that
of the exact solution. In this case the problem arises because of a spurious
solution of the difference equation corresponding to the root 
of 
. However
the problem can also arise in one-step methods which have no spurious solutions.
The polynomial
is called
the stability polynomial of the method. One of the roots 
will correspond to the true solution, the other roots will lead to spurious
solutions whose magnitude will have to be controlled to obtain stability.
Definition – Absolute Stability
A numerical method is said to be absolutely stable for a given 
if
all the roots of 
lie within the unit circle.
A region 
of the complex plane is said to be a region of absolute stability
if the method is stable for all 
in .
(a) Euler's method,
(b) Trapezoidal method.
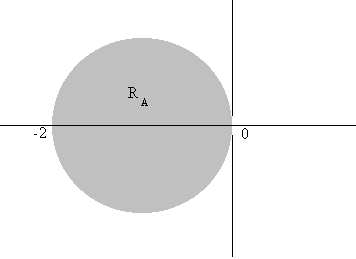
(a) For Euler's method
Thus
is shown
below
(b) For the Trapezoidal method
Thus
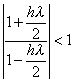
giving the region
shown below
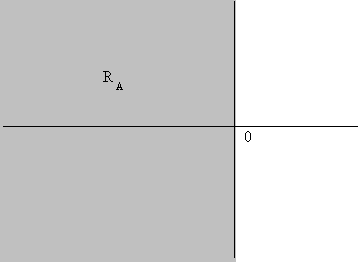
For Runge-Kutta methods the stability polynomial has the form
where 
is a polynomial for an explicit method and a rational function for an implicit
method.
where
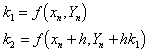
The stability polynomial is
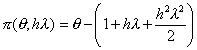
For absolute stability we require that
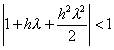
In order to draw the region of absolute stability consider the boundary
of 
. The
locus of this boundary will be the set of complex numbers z such
that
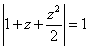
Thus
In order to obtain the region we need to plot the roots of the quadratic equation
for 
in the range 
.
This is best done on a computer. The resulting stability region is shown
below:
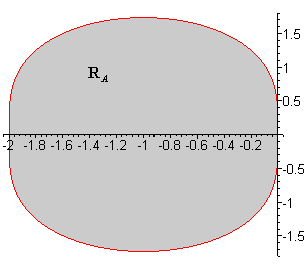
The method outlined above is an example of the boundary locus method which is easily implemented for Linear Multistep methods as follows. The stability polynomial is
and hence
but on
Hence the locus of the boundary 
is given by the set of complex numbers z satisfying
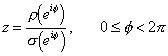
The stability polynomial is given by
Substituting 
and solving
Now substitute 
to obtain
which gives the plot
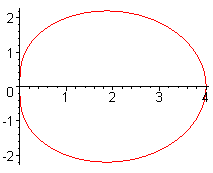
In order to determine whether 
is the interior or exterior of the closed curve choose a point inside the
curve and evaluate the roots of 
.
In this case
consists of the exterior of the closed curve.
has an empty region of absolute stability.
From above
Thus the stability polynomial is given by
Substituting
and solving
Now substitute
to obtain
which does not bound any region of the complex plane. Hence
is empty.