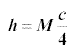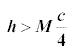- The harvesting occurring during the exponential growth phase follows the results obtained previously;
- As the population approaches equilibrium, we can take theevalue of
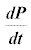 to be zero.
to be zero.
It is possible to obtain long term harvesting rates easily for the logistic model by making two assumptions.
From the logistic equation, the last assumption leads immediately to the result
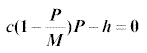
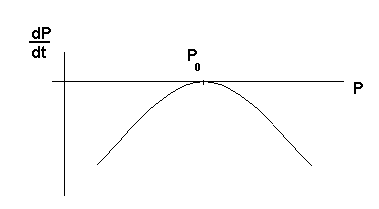
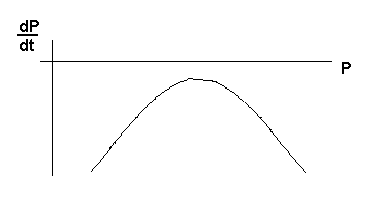
This is simply a quadratic equation in P, the population. Clearly, the roots of this equation must be real for the population to actually exist. We have:
cP2 - McP + Mh =0 whose solution is given by
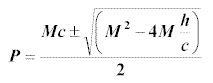
For real fish, we require real roots so that 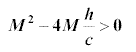
This leads immediately to the condition 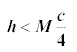
Hence the admissible harvesting values are given by the inequality 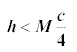 .
.
Notice that as ![]() the population
the population 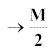 ,
which is half that of the totally unharvested population.
,
which is half that of the totally unharvested population.
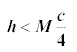
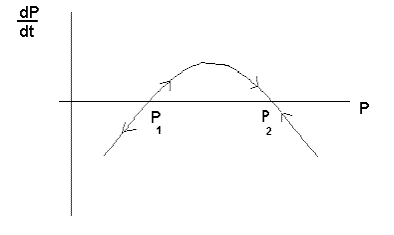
Evidently, P1 is unstable equilibrium point whereas P2 is stable.