- there exists a unique positive value of
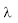 say
say 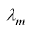 with the property
that the corresponding eigenvector x0 can be thought
of haa having only non-negative elements;
with the property
that the corresponding eigenvector x0 can be thought
of haa having only non-negative elements; 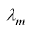 has the greatest
absolute value of any eigenvalue in the system.
has the greatest
absolute value of any eigenvalue in the system.
The properties are:
From a modelling point of view, Property 1 tells us that the Leslie
model will always give a population distribution consisting of positive
numbers only. This is important since it is impossible to consider populations
with negative or complex numbers of animals! Property 1 also states that
the age distribution is unique since ![]() is unique. Property 2 tells us that we can easily find the value of
is unique. Property 2 tells us that we can easily find the value of ![]() by finding the eigenvalue with the greatest absolute value. Packages such
as Maple will find the complete eigensystem of a matrix so that it is easy
to pick out the value of the eigenvalue
by finding the eigenvalue with the greatest absolute value. Packages such
as Maple will find the complete eigensystem of a matrix so that it is easy
to pick out the value of the eigenvalue ![]() and the corresponding eigenvector x0.
and the corresponding eigenvector x0.