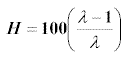
where H is a percentage of the total population.
Note that the above results will apply to any Leslie matrix model of
a population.
Exercises
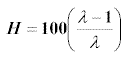
where H is a percentage of the total population.
Note that the above results will apply to any Leslie matrix model of
a population.
SOLUTIONS
Problem 1
Assume that the initial population is p0 and that the population after n time periods is pn. We know that the population after one year is Mp0 where M is our Leslie matrix. In general we have:
p1 = Mp0
p2 = Mp1 = M2p0
.
.
.
pn = Mpn-1 = Mnp0
But
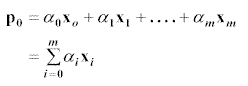
where xi are the eigenvectors of M.
HHnce 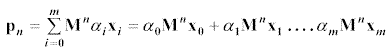
where ![]() are the
eigenvalues of M.
are the
eigenvalues of M.
But for every corresponding eigenvalue ![]() and eigenvector x0 we have
and eigenvector x0 we have
![]() so that
so that ![]()
and in general ![]() and so pn may be written as
and so pn may be written as
![]()
One eigenvalue, say ![]() is dominant so that we may factor
is dominant so that we may factor ![]() from each term and write
from each term and write
Hence, 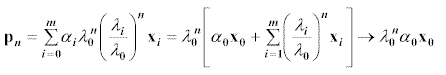 as
as
![]()
The limiting population is given by taking the limit ![]() as so that all the terms except the first approach zero.
as so that all the terms except the first approach zero.
We can now write
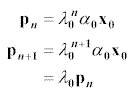
so that we have
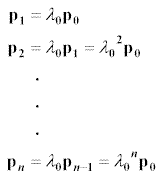
This shows that we are multiplying our initial population by a constant
factor (![]() ) and
so the population increase is exponential with a natural rate of increase
r given by
) and
so the population increase is exponential with a natural rate of increase
r given by ![]() .
.
Hence
![]()
The rate of increase of the population will be positive if ![]() .
.
The population will remain static if ![]() .
.
Problem 2
Assuming an appropriate value of ![]() ,
the population will increase from N to
,
the population will increase from N to ![]() ,
this is clear from Problem 1.
,
this is clear from Problem 1.
Hence the harvesting is given by the expressions
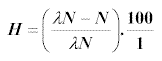
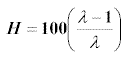
Problem 3
The exact results depend on your harvesting strategies - there is no simple correct answer to modelling problems which require you to decide on a strategy and implement it!