Chapter 3

ACTIVITY CYCLE DIAGRAMS

Activity cycle diagrams (ACD) are the natural way to represent the activity paradigm of discrete event simulation. They are particularly appropriate for problems with a strong queuing structure. Their utility however is not limited to queuing systems and the logical internal structure of the method makes ACD's a natural choice for model design specification. Whilst all real systems may be represented by ACD's the representation becomes over complex for some systems.

Basic definitions

If asked to describe a situation or problem which is to be the subject of a simulation modelling study the majority of people would intuitively follow a process description in which each important step is described consecutively. The reason for this is clear when you think about the way, for example, we would describe an activity such as joining a queue to by a train ticket. Our thought naturally follows through the sequence of steps or process required to purchase the ticket. However for more complex problems which we may be asked to model and perhaps in a context with which we may not initially be familiar there are disadvantages to this approach. We need to feel confident that our conception of the problem is logically consistent and complete in all important respects. With the process description neither of these requirements is met. If more than one person is involved in defining the logic of the model (at a minimum a study usually involves at least one analyst and one client) it would also be clearly an advantage if all contributors used a common easily understood descriptive language.
It is with these considerations in mind that the activity cycle description was evolved by xxxxxxxxxxxxx in xxxxxx. Whilst no descriptive language can ensure model completeness or validity a simple, logically self consistent model description language based on a few common symbols is clearly an advantage in describing complex systems. Whilst modelling languages exist which can translate an activity diagram directly into executable code (see section xxxx) it has to be admitted that the majority of languages are firmly routed in the process description paradigm. Thus having developed our model description as an activity cycle diagram we are faced with the task of translating this into a process description for computer simulation. However this task is really no more complex than, for example, translating a data flow diagram into computer code, an every day task for computer programmers.
Our explanation of activity cycle diagrams (ACDs) begins with the concept of an entity. In this context an entity is any item whose change of state (between used and not used or idle and active) can influence the occurrence of events within the model.

Example 3.1

When a couple order a meal in a restaurant we may consider the following entities to be required : the couple, the menu, the waiter and space at a table.
Notice from the example that entities can be people, objects or even abstract concepts like 'space at a table'. An entity may require a set of attributes for its complete description. As the entity progresses through the model it transports its attribute set with it. Thus an aircraft will have fixed attributes such as 'seating capacity' or 'maximum range' and variable attributes such as 'number of passengers' or 'route'. An entity will, of course, have a very large range of descriptive attributes (e.g. the aircraft has a 'colour' and a 'date of manufacture') but these are not considered unless important for model logic.

In an activity cycle diagram entities come together to engage in activities and when the activity is complete the entities move on to reside in a queue until required for another (or repeat of the same) activity. Thus we see that if we follow the progress of any entity within the model it will be seen to pass through an alternating sequence of activities and queues. In other words only two symbols are required to be represented in the model : a queue and an activity, usually represented by a circle and rectangle respectively.

Some entities reside entirely in the model throughout a simulation and so it is clear that their activity cycle will be a closed loop. Other entities reside only for a fixed period within the confines of the model.

Example 3.2

In the restaurant model the waiter, menu and table space reside permanently within the model. Customers arrive, order a meal, eat the meal, pay for the meal and depart.

To be logically consistent we consider all activity cycles to be in the form of closed loops. To achieve this for entities which enter and leave the model domain we need to add a special queue, the world queue, within which they reside when 'off stage' from the model domain. We also add a special 'arrival activity' which describes the arrival times of entities within the model. The arrival activity is an example of a 'time limited' activity which will be considered in more detail in section 3.3.2 but for now we note that it is given a special activity symbol as follows


Figure 3.1: The arrival activity

Not all queues have equal status within the model. For example in a drilling operation the work piece may require an operator to set it up on the drill but once the drilling operation is underway the operator is no longer required. This small scenario can be represented by the model fragment illustrated in

figure 3.2.

Q4 is a real queue where work pieces wait either for space on the drill or the availability of the operator. Likewise Q5 and Q6 are real queues in the sense that they represent the 'idle' status of drill and operator. The open circle however is an example of a dummy queue included essentially to maintain the alternating sequence of queues and activities. It is a dummy queue because the work piece will in fact move smoothly from the activity 'SETUP' to the activity 'DRILL' without pause.

The usual convention represents dummy queues by open circles.

The duration of an activity is usually defined at the time the activity starts and thus an 'end of activity' event can be defined. However it is possible that an entity may be pre-empted from an activity (which would then cease) by an activity of higher priority. After the higher priority activity has been completed the interrupted activity may be resumed at the point at which it was interrupted, restarted from the beginning or never restarted.

Figure 3.2 : Real and dummy queues

Example 3.3

The activity 'board aircraft' in an airport model may be pre-empted by the activity 'security check'. Subsequent to the completion of the security check the activity 'board aircraft' is re-started from the beginning.

In a hospital model the activity 'feed patient' may be pre-empted by the activity 'cardiac arrest'. Regretfully after completion of the activity 'cardiac arrest' the activity 'feed patient' may never be restarted.

Figure 3.3 illustrates the activity cycle diagrams associated with the three responses to a pre-emption activity (HPA).

Figure 3.3: The pre-empted activity

Note 1 In 3.3(a) Q3 may be Q1.

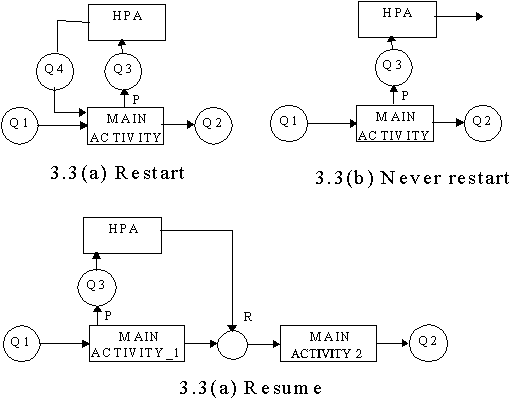
Note 2 HPA or High Priority Activity in Fig.3.3 could be a complete subset of entity cycles

3.2 Developing the activity cycle diagram.

The methodology for constructing an activity cycle diagram consists of the following five steps :

  1. Specify the model domain.

  2. List all entities and their key attributes

  3. For each entity define its individual closed cycle of activity - queue - activity

  4. Merge the individual activity cycles

  5. Verify the logic of the diagram and amend as necessary.

We can follow these steps through by taking as an example a basic restaurant model :

1.Specify the model domain

A restaurant employs a head waiter to accept customers, show them to the table and finally, when the customers leave takes the payment for the meal. A normal waiter serves meals to customers. Customers wait to be shown to their table and after finishing their meal wait at the table until they have paid for the meal. The purpose of the model is to ascertain the number of waiters required and, during the busy evening period the time customers must wait to be seated.

2. List all the entities and their key attributes

List all entities and their key attributes which are to be considered part of the model. Clearly the model must contain a 'head waiter' a set of normal 'waiters' and a set of 'customers'. A little reflection shows us that the model is unlikely to function correctly unless we also model 'table space'. Key attributes can be identified at this stage for example.

Customers : Number in the group, arrival time at the restaurant.
Head waiter : Time to complete payment by cash or credit card.
SAQ 1

Complete this list.

3. For each entity define its individual closed cycle of activity - queue - activity





Figure 3.4 : The individual cycles

4. Merge the individual activity cycles

Merge all individual cycles into a single activity activity cycle diagram by identifying common activities between cycles. If, at this stage an entity cycle is found which cannot be merged into the diagram you should question the definition of its activities, or the need for this entity.

This process begins by identifying common activities between cycles. For example the activity 'take order' for the waiter is clearly the same as the activity 'give order' of the customer. The same is also true for the activities 'serve meal' and 'receive meal'. The allows us to begin to merge two of the individual cycles (Fig. 3.5)

It is now possible to begin to see how an activity cycle diagram is used. Any activity will start as soon as the required number of entities are available in the preceding queues. In Fig. 3.5 as soon as a customer resides in the 'wait to ord.' queue and a waiter is in the idle waiter queue the activity 'give order' will commence. On completion of the activity the entities move on to their respective next queues. In this case the customer moves to the 'wait meal' queue and the waiter returns to the idle waiter queue. Fig 3.6 shows, at this stage, the completed activity cycle diagram.

Figure 3.5 : The merging of two cycles

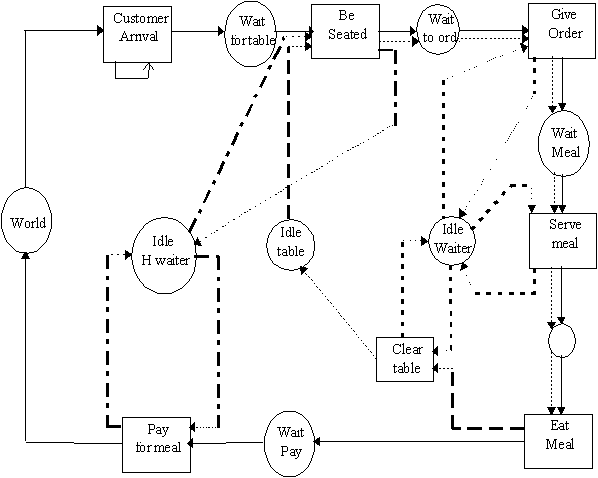
Figure 3.6 : The completed activity cycle diagram

5 Verify the diagram logic

Having completed the diagram it is necessary to verify that the logic is correct and the model will behave in the desired way. The verification is most easily achieved by 'walking through' sections of the model. This can be facilitated by using counters to represent entities. Whenever the requisite number of counters exist in the preceding queues they can all move to the activity which then takes place for the requisite time.
SAQ 2

Figure 3.5 is correct as regards setting up alternating sequences of queues and activities but does contain a serious error of design. Work through the logic to find the error and then correct the diagram.

3.3 Feature modelling

3.3.1 Arrival Activities

We mentioned earlier that the arrival activity was rather special. You can see that this must be the case because the activity only requires entities in the world queue before commencing and since, by assumption, the world queue contains an infinite number of entities of each type we appear to have no control over the arrival time. To solve this problem we create a single artificial entity which we will call 'gate'. Its activity cycle interacts with the arrival activity as shown in figure 3.4

Figure 3.7 :

'Hold gate' retains the gate entity for the inter-arrival time and during this time the system entity is unable to leave the world queue. On completion of its hold the gate passes through the dummy queue and together with a system entity from 'world' enters the 'arrival' activity. The arrival activity is of zero duration allowing the system entity to immediately enter the model. The gate entity returns to the 'hold gate' activity where it is held until the next arrival time.

Every arrival activity is of this form and so it is not normally represented on the diagram, its presence being indicated by the loop below an arrival activity.

3.3.2 Time Limited Cycles

The arrival activity is a special case of a time limited activity with a single period (the inter-arrival time). Many instances exist where we need to model multi - period time controlled activities.

Example 3.4

At a certain point on the coast the period of 'high water' is 5 hours followed by a 'low water' period of 7 hours.

A traffic light system is green for 5 minutes, amber for 30 seconds and then red for 5.5 minutes.

The first example is a two period time limitation and the second a three period limitation.

To model time limitation we extend the method used for the arrival activity. Fig. 3.5 shows, using the tidal example above, the activity cycle for a two period time limited system.

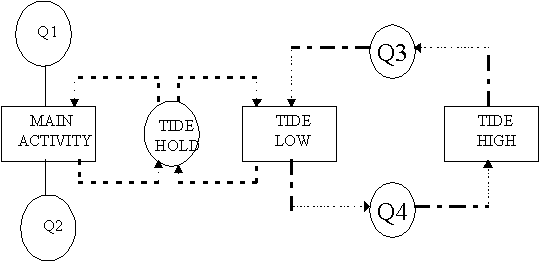
Figure 3.5

The two period cycle requires two tokens which in the context of this example we can label 'tide' (red) and 'moon' (blue). The moon token spends 5 hours in the activity 'tide high' and during this period the tide token is in the queue 'Tide hold'. When in this queue, of course, it is available to control entity flow through the 'main activity' which can thus take place at any time during the 5 hour period. On completion of the activity 'Tide hold' the moon token moves immediately to the activity 'tide low' if the tide token is in the queue 'Tide hold' otherwise it waits in Q3 until the tide token is available. Once in the activity 'Tide low' of duration 7 hours the tide token remains unavailable for 7 hours and the 'main activity' cannot occur.

Thus we see that flow along the main cycle is controlled by a two period cycle as shown in Fig. 3.6

Figure 3.6


SAQ 3

There is a circumstance in which the above two period cycle will operate incorrectly. Identify the problem and suggest a solution. SAQ 4

Construct the activity cycle diagram for a three period time limited cycle.

3.3.3 Resource limited cycles

The restaurant model contained an example of resource limitation with the entity 'table space'. From that example you see that resource limitation can be modelled by adding an activity cycle which 'shadows' that part of another entity cycle where the resource limitation is significant. Usually resource limitation cycles are added to an existing ACD initially created on the assumption of the free availability of a resource. In the restaurant model the table space entity shadows the customer cycle from the activity 'Be seated' until completion of the activity 'Eat meal'.

3.3.4 Extended convention for activity cycle diagrams

As you will soon discover when you construct an activity cycle diagram for a real world problem the diagram can easiliy become large, spread over several sheets and with activities being connected to many queues. In this situation an extension to the diagram convention can improve readability. Attaching labels to queues and activities will also aid transforming the diagram into a simulatable form. For queues a convenient convention is shown in Fig. 3.7

Figure 3.7 : Diagram convention for queues

Each queue is given a name, number and a number to represent the maximum queue capacity.

For activites it is very useful to include the source and destination queue numbers for each entity taking part in the activity. We can also take the opportunity to include an activity number and a number representing the number of possible similar concurrent activities. For example if a single queue for components can feed any one of three lathes we can either have three separate lathe activites or use the convention and designate three concurrent activites. The activity number is also used to represent the 'priority' of the activity for obtaining resources with the lowest number having the highest priority. Fig. 3.8 illustrates the convention.

Figure 3.8 : Diagram convention for activities

In the example the activity takes place when a printed circuit (PC) board is available in queue 12 and an operator in queue 2. The activity duration is normally distributed with a mean of 5 mins. and a standard deviation of 1 min. On completion of the activity the PC board moves to queue 37 and the operator returns to queue 2. Three similar activities can occur.

3.4 Language implementations of ACD

The original implementation of the activity cycle approach to modelling was a joint development in the U.K. between IBM UK and Esso. This became the first programmed version known as CSL (Control & Simulation Language, Buxton & Laski 1962). A successful further development of this has been ECSL (Extended Control & Simulation Language) by Clementson (1991). The current version of ECSL runs on a variety of platforms including IBM PC's and the DEC Vax/VMS systems. In addition to the program generator and compiler the system now includes a number of support tools to enable a user to link ECSL to particular editors and spreadsheet packages for analysis. In its pure form the language now has a fairly primative feel to it. Consider for example the following example of a simple queueing system coded in ECSL

  1. BEGIN SERVE CUSTOMER
  2. FIND FIRST SERVER S IN IDLE
  3. FIND FIRST CUSTOMER C IN WAITING
  4. DURATION = 23
  5. SERVER FROM IDLE INTO IDLE AFTER DURATION
  6. CUSTOMER FROM WAITING INTO SERVED AFTER DURATION
  7. REPEAT

On reading this it is not difficult to imagine the underlying fragment of an activity cycle diagram or to see the operation of the three phase simulation methodology. However the majority of current simulation packages do not force the developer to write a structured program. The more common approach is to use graphical tools to build the model.

CAPS or Computer Aided Programming Tool is an ECSL program generator which enables the user to enter activity cycles directly into the computer and CAPS will then generate the appropriate ECSL code. Whilst this is not a graphical input tool it does at least represent the activity cycles directly. The user is led through a structured dialog for each cycle of which the following is a typical example :
System User response
PROBLEM NAME ?pub
DO YOU WISH TO START A NEW PROBLEM?yes
ARE YOU GOING TO USE IMPLICIT QUEUE MODE?no
LOGIC
TYPE NAME OF ONE KIND OF ENTITY?customer
HOW MANY?10
TYPE A LIST OF THE STATES THROUGH WHICH THESE ENTITIES PASS
PRECEDE QUEUES BY Q AND ACTIVITIES BY Aqoutside
aarrive
qwaiting
apour
qready
adrink
qwaiting, cneed>0
qoutside

This discribes the activity cycle of a customer entering a pub drinking one or more drinks and then leaving the pub. All activity cycles are entered in a similar way. the program is then able to analyse the ACD logic and compose the complete diagram. A considerabel amount of other data (e.g. activity priorites, number of entities used per activity, calculations, statistical functions tec.)

A similar approach is taken by HOCUS (Hand or Computer Universal Simulator) which uses a modified version of the activity cycle approach. The first step of using HOCUS for the user is to sketch an activity cycle diagram. The user is then asked to submit a description of the diagram to the computer. The original HOCUS data entry format was based on the old 80 column punched card layout but the latest versions have provision for visual interactive modelling. HOCUS is available on quite a wide range of platforms including the IBM PC, Xenix, SunOS etc.

3.5 Use of ACD in model specification.

We do not anticipate that the majority of users of discrete event simulation are going to work exclusively with the activity cycle paradigm. However we believe in the design phase of the simulation project the paradigm can make a valuable contribution.

3.5.1 Structured walk- throughs

Usually the simulation analyst will be developing a model of processes with which, at the outset, he will not be totally familiar. He needs to develop an accurate understanding of the dynamics of the problem domain. Developing an activity cycle diagram of the system with its rigid low level logical structure is a very good way of achieving this understanding. Having developed the ACD the analyst can then hand simulate crucial parts of the model by moving counters to represent the entities over the diagram and calculating timings and queue sizes etc. This will readily reveal logical errors (such as missing tokens) in the model. We find that after a brief explanation the regular users of the system being simulated can understand the paradigm sufficiently to confirm or correct short sequences of events

3.5.2 Verification planning

Once a simulation model has been developed the next crucial phase is verification. Again the ACD has a role to play in the design of verification procedures. In a reasonably complex model it is not possible to test every possible event combination that may arise during the simulation run. Modern languages contain relatively sophisticated features such as the WAIT - SIGNAL combination in SIMAN where a signal issued (or not issued !) at one point in a model can have a dramatic effect in a far distant part of the model. We have known combinations appear in a large model (containing several thousand entities concurrently) after several months of successful operation which have generated a run time error.

The ACD can be used to identify the crucial event combinations and the expected outcomes from these combinations. These can then be included in the test programme.

If a run time error is detected the ACD can be used in combination with the simulation languages 'trace' or 'debug' facilities to track the source of the problem down and to suggest a possible solution.

3.5.3 Conversion to process orientation

If a comprehensive ACD has been developed it seems natural to translate this to the process paradigm for computer implementation. This involves selecting 'Primary entities' in the ACD which will become the entities which move through the process simulation and 'Secondary entities' which will become resources 'seized' by the primary entities.

Hard and fast rules are difficult to define for this process but some general principles can be stated.

3.6 Limitations of activity cycles.

Whilst, as we have seen, it is quite possible to carry out a computer discrete event simulation through the activity cycle paradigm and 4GL's exist for this purpose it remains true that the great majority of computer based simulations use the process paradigm. Why should this be so ? Three principal reasons can be identified for this all of which are reinforced by recent trends.

  1. ACD's are not an intuitive paradigm. Increasingly process language implementations are appearing which claim to allow the non specialist user to develop simulations through graphical interfaces. In such systems the user is not even confronted with the problem of learning a language syntax. It is natural for the user to want to model in the paradigm she uses to think about the real system which is almost invariably the process paradigm

  2. Animation facilities now form a major part of most packages. Whilst it is quite easy to animate an activity cycle model such an animation would not in its simplest form correspond to an observers view of the real system. Such a view can be achieved but at the expense of considerable extra work compared, for example, to packages such as ARENA or WITNESS where the animation is almost an inevitable byproduct of building the model.

  3. The efficiency of many current languages is increased by the use of object orientated concepts. Even at its lowest level this involves structured elements which in a single model construct can represent a complex sequence of activites and queues. Thus a few model constructs may describe a complete conveyer system or an automatic guided vehicle transport system. In its pure form the ACD concept is directly opposed to these trends.

3.7 Workshop problems

    1. A cross roads is fitted with traffic lights operating in the sequence shown below for the East - West (EW) and North - South (NS) roads. The timing of the lights is not effected by the traffic flow. Including traffic on the two roads develop an activity cycle diagram for the operation of the junction
NS
EW

3.8 Solutions to SAQ's

SAQ 2

The customers will never reside in the 'wait meal' queue if a waiter is available because, apart from the waiter, all required entities are present in the queue. Thus it is not possible to model the delay occurring whilst the meal is prepared. The solution of course is add an activity cycle for the meal. Do this now.

SAQ 3

If the duration of the main cycle activity is a significant fraction of the two cycle period then the phase of the two cycle period will change in response to activity in the main cycle. The solution, of course, is to add a special activity to the main cycle which has a zero duration and whose only function is to act as a 'gate keeper' for flow along the main cycle.