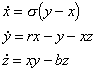
The celebrated dynamical system due to Lorenz which describes the motion of a fluid in a horzontal layer which is being heated from below has the form

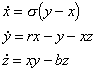
where x represents the velocity, y and z the temperature of the fluid and  are positive parameters determined by the heating of the fluid, the physical properties of the fluid and the height of the layer.

The equilibrium points of the system are

The equilibrium point at the origin is stable if  and unstable if .

The other two equilibrium points, which only exist if  are stable if  and unstable if  where

Maple Analysis

• Worked Example 1

Maple Solution

• Worked Example 2

for the Lorenz equations.

Maple Solution

The original parameter values used by Lorenz were . For these values of  and r the critical value of r is given by .

The plots below show a trajectory and an x v. t time series plot of the system with initial conditions .

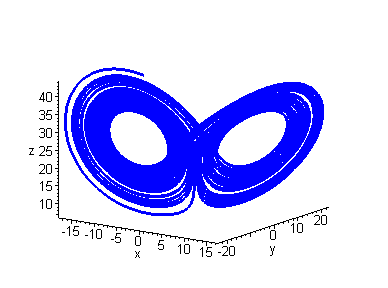
Note that the solution trajectories encircle first one equilibrium point and then the other. This pattern of motion is repeated endlessly with the trajectories being confined to a strange attractor. The time series plot indicates the apparently random nature of the motion.

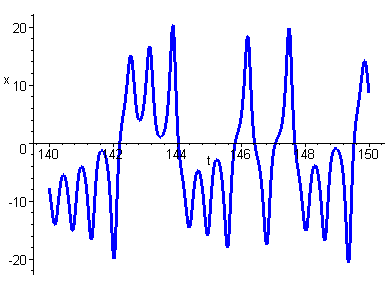
The plots below show time series plots at  for slightly different initial conditions

Note that the two plots are completely different despite the very small (0.1%) change in the initial condition for x. This type of behaviour in which a small change in the initial conditions can produce a large change in subsequent values is called sensitive dependence on initial conditions also commonly referred to as the butterfly effect. This is a characteristic of chaotic dynamical systems.

The link below provides a Java simulation of the system.

Java Simulation

Parameter values and initial conditions can be changed.

An alternative series of simulations is available using Maple.

Maple Simulation