![]()
The results of Worked Example 1
can be formalised in the following theorem.
Let D be a closed bounded region of the x-y plane and
![]()
be a dynamical system in which f and g are continuously
differentiable. If a trajectory of the dynamical system is such that it
remains in D for all ![]() then
the trajectory must
then
the trajectory must
(i) a closed orbit,(ii) approach a closed orbit or
(iii) approach an equilibrium point as
.
The implication of this theorem is that if we can find a trapping
region for a dynamical system which does not contain an equilibrium point
then there must be at least one limit cycle within the region. The technique
of transforming to polar coordinates although often employed does not always
work. The following examples demonstrates other methods of obtaining trapping
regions.
![]()
where x and y are concentrations of reactants and a and b are positive parameters.
The diagram below shows the graphs of the expressions
![]()
and
![]()
on which ![]() and
and ![]() respectively.
The region within the dotted lines is a trapping region for the system.
respectively.
The region within the dotted lines is a trapping region for the system.
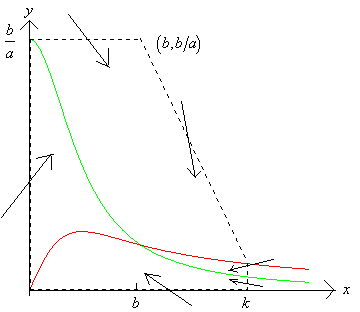
However we cannot conlude that there is a limit cycle within region
since the equilibrium point ![]() lies
within the region.
lies
within the region.
The Jacobian matrix of the linearzation is
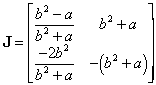
Now ![]() and
and
![]()
If we choose the parameters a and b so that ![]() then
the equilibrium point will be a repeller. In this case suuround the equilibrium
point by a small circular region as shown below.
then
the equilibrium point will be a repeller. In this case suuround the equilibrium
point by a small circular region as shown below.
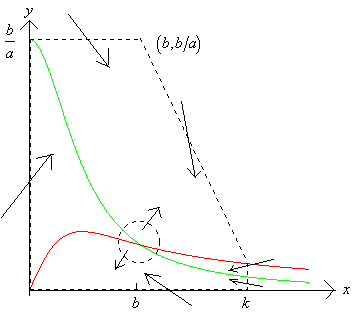
Since the equilubrium point is a repeller, trajectories crossing the boundary must point into the region defined by the dotted lines. In this case the new region is a trapping region which does not include an equilibrium point. Thus the Poincaré-Bendixson theorem guarantees that the region must contain at least one limit cycle.
We can verify this result using Maple to obtain the phase portrait.
Suitable parameter values are ![]()
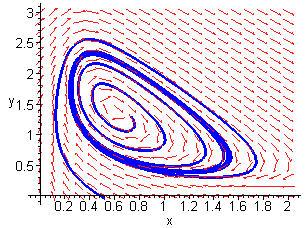
Limit Cycle
![]()
on the trajectories of the dynamical system
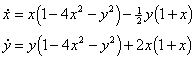
show that the dynamical system has a stable elliptical limit cycle.
It is easily seen that the only equilibrium point of the system occurs at the origin.
Now
![]()
Thus we see that V decreases on the trajectories except at the
origin where it clearly has a relative maximum, and on the ellipse ![]() where
it is identically zero.
where
it is identically zero.
Consider the plot of V shown below
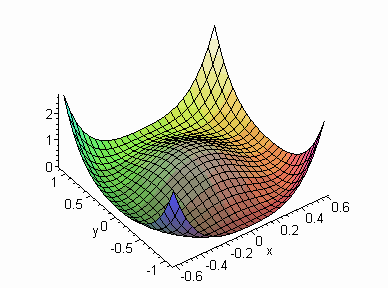
Outside the ellipse the function is decreasing towards the ellipse. Inside the ellipse the function is decreasing towards the ellipse again. Thus the trajectories of the system must move towards the ellipse from points outside and inside for increasing t.
Now consider a contour plot of V
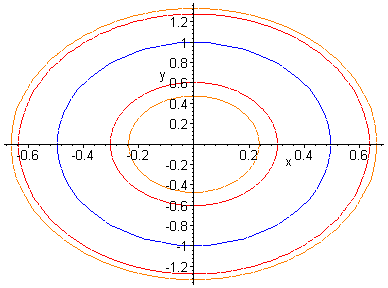
We can construct a trapping region by taking any contour inside the ellipse as the inner boundary of an annular region together with any contour outside the ellipse as the outer boundary. Hence by the Poincaré-Bendixson theorem since there are no equilibrium points within the annular region there must be a stable limit cycle within the region.
Note also that as the contours can be taken as close to the ellipse as we like the limit cycle must be the ellipse.